
![]()
Yapay Sinir Ağları ve R Programıyla Uygulama
Artificial Neural Network
Utku Kubilay ÇINAR
Yapay sinir ağları (YSA), insan beyninden esinlenerek geliştirilen ve günümüzde kodlama dünyasında sıklıkla kullanılan bir algoritmadır. Bir yapay sinir ağı, yapay sinir hücreleri arasında çeşitli bağlantılarla oluşur. Oluşan bu bağlantılar arasında önem (ağırlık ya da insan beynindeki “sinapslar”) vererek sonuca ulaşmayı amaçlar. Yeni bilgiler keşfetmekte ya da verilerin modellenmesinde dışarıdan yardım almadan, makine kendi kendine öğrenerek belirlenmiş amaca ulaşan bilgisayar (algoritma) sistemleridir.
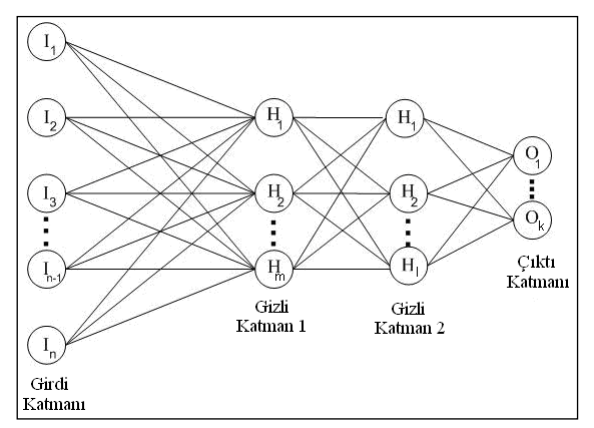
Yapay sinir ağları modellemesinde giriş (x), çıkış(y) değişkenleri arasındaki ilişki y=f(x)+Hata şeklindedir. Burada hatayı(error) azaltmak için ağırlık(weight)(W) bilgileri ayarlanır ve atanır. Buradaki amaç girdilerin önemine göre bir işlem yaparak, girdilerle işlemi yapmaktır(aktivasyon fonksiyonu). Bir yapay sinir ağında gizli düğüm ya da düğümler olabilir. Model içinde veya giriş ve çıkış katmanları arasında gizlenmiş bir katman ve çevre ile doğrudan bağlantısı olmayan bir katman olabilir. Yapay sinir ağlarının avantajlarından olan bu işlem, yapıyı anlamamızda araştırmacıya kolaylık sağlar.

Bir yapay sinir ağları hücresinin yapıları ise; girdiler, ağırlıklar, toplama fonksiyonu, aktivasyon fonksiyonu ve çıktılardır.
Yapay sinir ağları(YSA)’ nın temelinde girdiler arasında bağlantıları oluşturan esas elemanlardan, bağlantı ağırlıklarının belirlenmesinde öğrenme algoritmalarından fonksiyon oluşturmaktır. Her eleman birbirlerine veri setindeki önemine göre ağırlıklarla bağlıdır. Bu ağırlıklar ise, o iki elemanın bağlantı gücünü gösterir.
Yapay sinir ağları, veri yapısına göre çok katmanlı olabilir. Zaman serilerinde bu durum sıkça karşımıza çıkmaktadır. Gizli katman sayısını ve yapısını belirlemek gerekir. Ağın toplam kaç adet basamaktan oluşacağı, bu basamakların (katmanların) kaç işlem yapacağı, kaç farklı katmana ne kadar ağırlıkla bağlanacağı gibi değerlerin belirlenmesi gerekmektedir. Bu işlemlerle birlikte yapay sinir ağları oluşturulmuş olur. Eğer tahmin modeli oluşturulacaksa yapay sinir ağlarından, bundan sonra yapılması gereken durum kaç tane öngörü yapacağını belirtmek olacaktır. Belirlenen öngörü sayısına(dönemine) göre çıkış nöronu belirlenir.
Yapay sinir ağları, ileri istatistiksel yöntemlerine karşı veri seti için herhangi bir varsayıma ihtiyaç duymaz. Yapay sinir ağlarının temel özelliği ve görevi, veri setindeki yapıyı öğrenmek ve istenilen göreve göre genelleştirmeler yapmasıdır. Bunu yapabilmesi için eğitim veri setinin üstünde çalışarak ağırlıkları belirlemesidir. Böylece her bir gözlemle ağırlıklar değişerek zamanla daha güclü ve sapması azalan bir yapıya dönüşecektir. Böylelikle çıktı olarak verdiği tahminde ya da yapıda genelleştirme yeteneği daha güclü olacaktır. “Ağın ürettiği sonuçlar ise; ağa girilen bilgilerin kendi ağırlıkları (W) ile çarpımlarının toplanması sonucu elde edilen net girdinin, bir transfer fonksiyonu ile işlenmesi ile çıktı katmanından alınmaktadır.”Öztemel, E., (2003)

Yapay sinir ağlarında yapının kaç gizli katmandan oluşacağı ya da kaç tane nöronla birleşeceği gibi sayıların belli bir kuralı yoktur. Burada bu sayıları belirlerken deneme yanılma yolu ile belirlenir. Bu çalışmada validasyon işlemleri ile bu sayı belirlenmeye çalışılacaktır. Büyük yapılar için genelde bir ya da iki gizli katman sayılarının yeterli olacağı literatürde belirtilmiştir. Tekrar belirtilmelidir ki bu sayıları belirlemek için bir formül olmadığından test edilerek belirlenmelidir.
Yapay Sinir Ağları 2’e ayrılır:
- İleri Beslemeli Ağlar: İleri beslemeli yapay sinir ağlarında aktarılan bilgiler sadece ileri doğru hareket eder yani girişten çıkışa doğru bir hareket söz konusudur. Bir katmandaki nöronlar sadece kendinen sonra gelen katmana gider, ardından sonuç(çıkış) katmanına geçer. İleri beslemeli yapay sinir ağları, giriş katmanındayken dışarıdan gelen bilgilere herhangi bir değişiklik yapmadan bir sonraki katmana aktarır. Bu süreç içinde bilgi, orta ve çıkış katmanında fonksiyonlarla belli bir ağırlığa sahip olur ve çıkış nöronuna yönlendirir.
- Geri Beslemeli Yapay Sinir Ağları: En az bir hücrenin çıkışı, diğer herhangi bir hücreye giriş olarak verilir bundan dolayı genellikle geri beslemeli yapay sinir ağlarında bir geciktirme eleman üzerinden yapılır. Besleme işlemi bir katmandaki hücreler arasında olmayabilir, bu sebeple doğrusal ilişkinin varlığından söz edilemez. Bu sebeple yapay sinir ağlarının geri beslemenin yapısı veri setine göre değişkenlik gösterebilir.
Çok katmanlı yapılara sahip yapay sinir ağlarında momentum katsayısı vardır. Ağların yerel sonuçlara takılmaması için momentum katsayısı kullanılır. Bu katsayı ile kabul edilebilir hata düzeyi alta çekilebilir fakat bilgisayar gücü bu konuda önemlidir. Çok katmanlı bir yapıda öğrenme oranı ile momentum ciddi işlem süresini uzatabilir. Momentum değeri, yerel çözümlere takılmayı engellerken sayısının küçük ya da büyük seçilmesine dikkat edilmelidir. Ayrıca bir önceki iterasyon değişiminin belirli bir oranının yeni değişim miktarını etkilemesidir.
Öğrenme oranı belirlenirken fazla bir oran girildiğinde problemi öğrenmekten ziyade verileri ezberler ve bu da veri setinin genellenebilme özelliğini kaybetmesine sebep olur ve hatalı sonuçlar üretilmesine neden olur.
Yapay Sinir Ağlarının Bazı Avantajları
- Yapay sinir ağları bir çok hücreden meydana gelir ve bu hücreler eş zamanlı olarak çalışarak karmaşık işlemleri gerçekleştirir.
- Yapı üzerinde dağılmış belli tipte non-lineer alt birimler, non-lineer problemlerin de çözümünü mümkün kılmaktadır.
- YSA’ lar makine öğrenmesi gerçekleştirebilirler. Olayları öğrenerek benzer olaylar karşısında mantıklı kararlar verebilir.
- Geleneksel yöntemlere göre daha hızlı ve literatüre göre daha başarılı tahmin(öngörü) yapabilmektedirler.
- Daha önce görülmemiş örnekler hakkında bilgi üretebilirler. YSA’lar eğitimleri sırasında kendilerine verilen örneklerden genellemeler çıkarırlar ve bu genellemeler ile yeni örnekler hakkında bilgi üretebilirler.
- Hata töleransı vardır.
Yapay sinir ağlarının kullanım alanları: Kontrol ve sistem tanımlama, görüntü ve ses tanıma, tahmin ve kestirim, arıza analizi, tıp, haberleşme, trafik ve üretim yönetimi olarak sayılabilir(Pirim, 2006). Günümüzde sıklıkla sınıflandırma, modelleme ve tahmin uygulamarları üzerine pek çok alanda yaygın olarak kullanılmaktadır. Makine öğrenimi algoritmalarının uygulandığı hemen hemen her alanda kullanıma elverişlidir.
Yapay Sinir Ağları Örnek Uygulaması- R Programı
Yapay sinir ağları çalışırken MASS kütüphanesi içindeki “Boston” veri seti üzerine çalışmalar gerçekleştirilmiştir. Boston veri seti, Boston banliyölerindeki konut değerleri hakkında bir veri topluluğudur. Amacımız, sahip olunan tüm diğer sürekli değişkenleri kullanarak sahiplenmiş evlerin (medv) medyan değerini tahmin etmek ya da belirlemektir.
# Kullanılan Kütüphaneler ( Pokemonlar )
library(MASS)
library(neuralnet)
library(nnet)
library(NeuralNetTools)
library(boot)
library(caret) library(corrplot)
library(DataExplorer)help(“Boston”) komutu ile veri seti hakkında detaylı bilgiye ulaşabilirsiniz.
set.seed(123) # rasgele sayı üretme fonksiyonudur. Rasgele seçimleri başlatmak için kullanır.
veri <- BostonBu kısımda veri seti, keşifçi veri analizlerinden bazılarıyla incelenecektir.
introduce(veri)## rows columns discrete_columns continuous_columns all_missing_columns
## 1 506 14 0 14 0
## total_missing_values total_observations memory_usage
## 1 0 7084 54944Veri setinde gerektiği durumda veri setinin sınıfını değiştirmek istenildiğinde ya da sınıfını görmek istenildiğinde plot_str() fonksiyonu ile tüm parametrelerin kategorileri görülebilir. Bu görseli istemiyorsanız eğer str() fonksiyonu ile de parametrelerin kategorilerini görebilirsiniz.
plot_str(veri)

Görüldüğü gibi veri seti 506 gözlem ve 14 parametreden oluşmaktadır ve 12 tanesi numerik, 2 tanesi ise integer haldedir.
Eksik gözlemlere bakıldığında eksik veri görülmemiştir. Bu işlemi yaparken apply fonksinoyu kullanılmıştır.
eksik_veri <- apply(veri, 2, function(x) sum(is.na(x)))
eksik_veri## crim zn indus chas nox rm age dis rad
## 0 0 0 0 0 0 0 0 0
## tax ptratio black lstat medv
## 0 0 0 0 0# Eğer görsel bir tablo içerisinde eksik verileri görmek istersek
plot_missing(veri)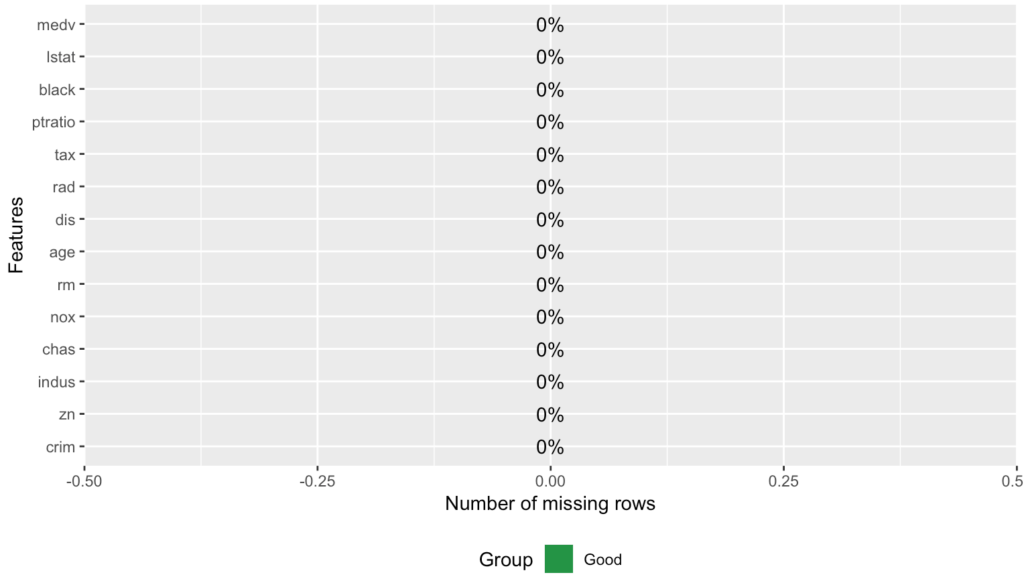
Veride eğer outlier (sapan-aykırı-uç değer) olsaydı şu fonksiyonu yazmamız gerekirdi. Bu fonksiyonun şu avantajı vardır; grafiği ikiye böldüğünü düşünün, sol tarafta aykırı gözlem varken ki hali, öbür tarafta ise aykırı değerlerin silinmiş hali gösterilmektedir. Kıyaslama açısından faydalı olabilir. Veri setimizde eksik gözlem olmadığı için bu işlemi yapmadan keşifçi veri analizine devam edilmiştir.
aykiri_deger <- function(dt, var) {
var_name <- eval(substitute(var),eval(dt))
tot <- sum(!is.na(var_name))
na1 <- sum(is.na(var_name))
m1 <- mean(var_name, na.rm = T)
par(mfrow=c(2, 2), oma=c(0,0,3,0))
boxplot(var_name, main="Aykırı Değer İçeren")
hist(var_name, main="Aykırı Değer İçeren", xlab=NA, ylab=NA)
outlier <- boxplot.stats(var_name)$out
mo <- mean(outlier)
var_name <- ifelse(var_name %in% outlier, NA, var_name)
boxplot(var_name, main="Aykırı Değerler Silinmiş")
hist(var_name, main="Aykırı Değerler Silinmiş", xlab=NA, ylab=NA)
title("Aykırı Değer Kontrolü", outer=TRUE)
na2 <- sum(is.na(var_name))
message("Aykırı Değer Tespit Edildi: ", na2 - na1, " den ", tot, " gözlemler")
message("Aykırı Değerlerin Oranı (%): ", (na2 - na1) / tot*100)
message("Ortalama Aykırı Değer: ", mo)
m2 <- mean(var_name, na.rm = T)
message("Aykırı Değerler Varken Ortalama: ", m1)
message("Aykırı Değerler Silindikten Sonraki Ortalama: ", m2)
response <- readline(prompt="Aykırı değerler yerine NA yerleştirilsin mi? [Evet/Hayır]: ")
if(response == "e" | response == "evet"){
dt[as.character(substitute(var))] <- invisible(var_name)
assign(as.character(as.list(match.call())$dt), dt, envir = .GlobalEnv)
message("Aykırı Değerler Başırılı Şekilde Kaldırıldı", "\n")
return(invisible(dt))
} else{
message("Hiçbir Şey Değişmedi", "\n")
return(invisible(var_name))
}
}Korelasyonlar incelenmek istenildiğinde corrplot kütüphanesindeki corrplot fonksiyonu ile korelasyonlar görselleştirilmiştir.
corrplot(cor(veri))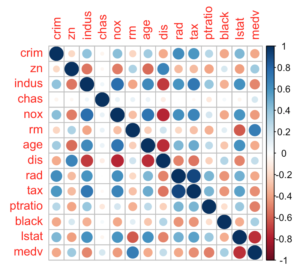
Keşifçi veri analizlerinden birkaç tanesine bakıldıktan sonra uygulamaya başlayalım.
Veri setinde ölçümler farklı olduğu için bu değerlerin aynı baremde birleşebilmesi için veri setinin normalize edilmesi gerekmektedir. Bunun için “scale” formulü kullanılır. Bu normalizasyon işlemini yaparken veri setinde her bir parametrenin maksimum ve minimum değerleri üzerine hesaplanarak gerçekleştirilmiştir. “Scale” fonksiyonu veri setinin karakterini bozmadan ortalaması sıfır, standart sapmasını bir üzerine merkezileştirerek veri setini günceller.
maxValue <- apply(veri, 2, max)
minValue <- apply(veri, 2, min)
veri <- as.data.frame(scale(veri, center = minValue, scale = maxValue - minValue)) Veri setimizdeki veri dönüşümü ve analize hazır hale getirdikten sonra veri setimizden Test-Eğitim verisini belirleyelim. Literatürde veri setinin % 70 Eğitim, % 30 Test ya da % 80 Eğitim, % 20 Test verisi olarak bölmek kabul görmüştür. Bu uygulamayı yaparken veri setini % 80 Eğitim ve % 20 Test verisi olarak bölündüğünde oluşan güncel veri setimizde 400 Eğitim, 106 Test verisi bulunmaktadır.
Rasgele örneklem seçerken “sample” fonksiyonu kullanılır. Eksik gözlem bulunmadığı için ve yanlı bir seçim olmaması için rasgele örneklem seçilmiştir. Belli bir sayı değil de belli bir oran üzerine bölmek isteseydik eğer şu kodu kullanmamız gerekirdi “sample(1:nrow(data),round(0.80*nrow(data)))” böyle rasgele olarak % 80 veri seti seçilmiş olurdu.
orneklem <- sample(1:nrow(veri), 400)
egitim_verisi <- veri[orneklem, ]
test_verisi <- veri[-orneklem, ]Seçilen test ve eğitim veri setlerinin uzunluk ve derinliğine bakaldığında toplam 14 parametre görülmektedir. Bunlardan medv parametresi bağımlı değişkenimizken diğerleri bağımsız değişkenlerdir.
dim(test_verisi)106 14dim(egitim_verisi)400 14Amacımız medv bağımlı değişkeni tahmin etmektir. Bunun için ihtiyacımız olan formul ise: “medv ~ crim + zn + indus + chas + nox + rm + age + dis + rad + tax + ptratio + black + lstat” olacaktır. Bu fonksiyon ile parametreler arasına otomatik olarak “+” eklenerek modele eklenecektir.
parametre_birlestirme <- function(resp, dt) {
nms <- names(dt)
fmla <- as.formula(paste(resp, "~", paste(nms[!nms %in% resp], collapse = " + ")))
fmla
}
duzeltilmis_veri <- parametre_birlestirme("medv", Boston)Gizli argüman, her bir gizli katman için nöronların sayısını içeren bir vektörü kabul ederken, “lineer.output” regresyon yapmak isteyip istemediğimizi belirtmek için kullanılır.
deneme_model <- neuralnet(duzeltilmis_veri
, data = egitim_verisi
, hidden = c(4,2)
, linear.output = T)plot(deneme_model)

Gizli sınıf katmanlarını deneme yanılma yoluyla deneyerek 2 farklı model kuralım. Biri 2 katmanlı olsun ve ağları ilk adımda 5, diğer adımda 3 olsun diğer modelimizde bir katmandan oluşsun ve 8 ağı olsun.
2 katmanlı birinci modelimiz oluşturalım.
model_1_nn_5_3 <- neuralnet(duzeltilmis_veri
, data=egitim_verisi
, hidden=c(5,3)
, linear.output=TRUE)2 katmandan oluşan modelimiz;
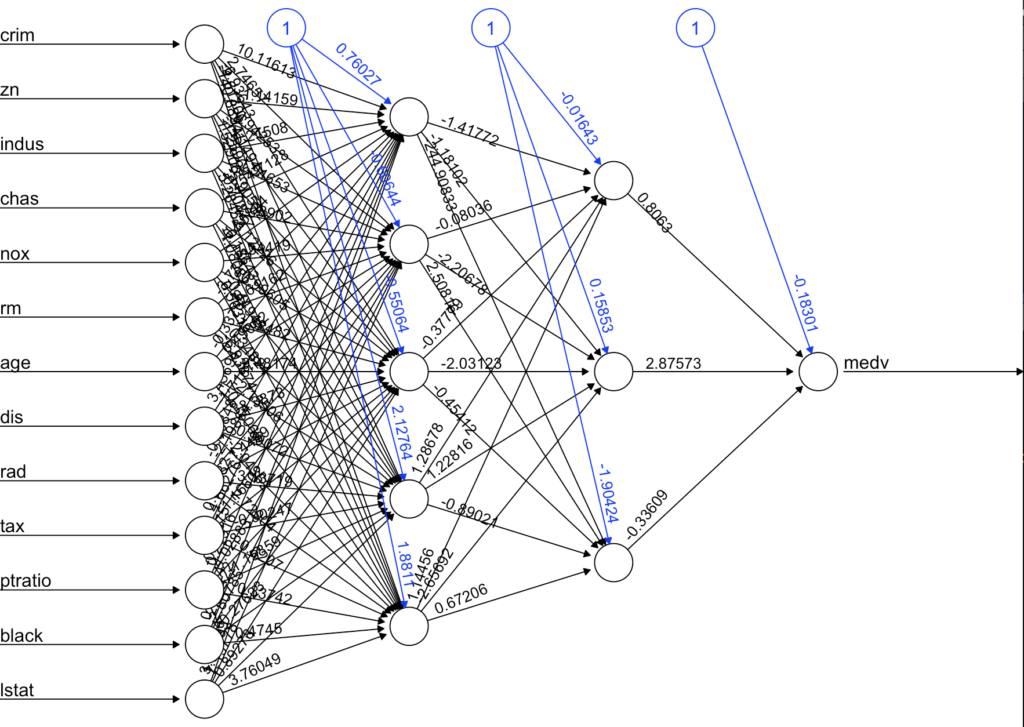
plot(model_1_nn_5_3)

Yapay sinir ağı modelimiz görüldüğü gibidir.
plotnet(model_1_nn_5_3)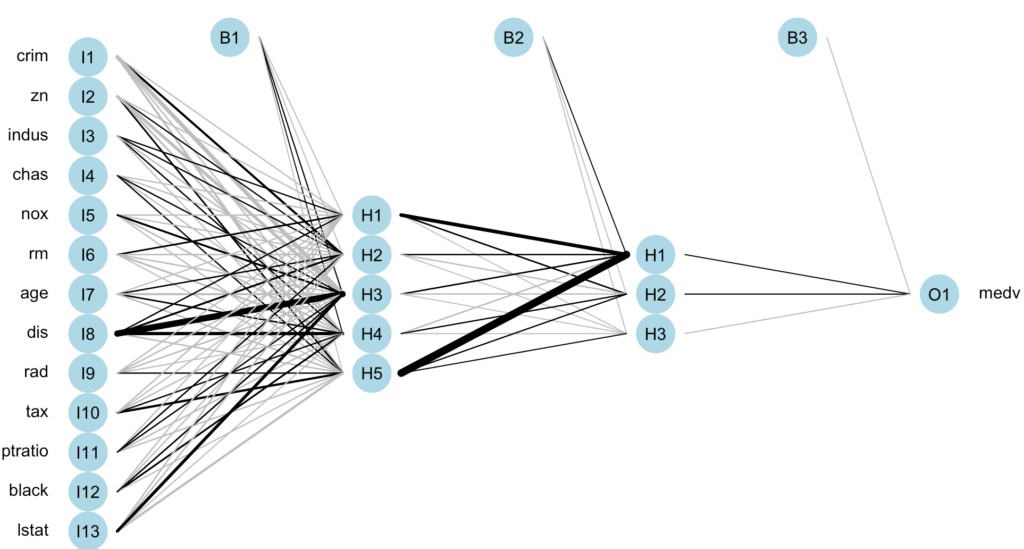
Tek gizli katmanlı ikinci modelimiz.
model_2_nn_8 <- neuralnet(duzeltilmis_veri
, data= egitim_verisi
, hidden=8,
, linear.output = TRUE)Tek katmandan oluşan modelimiz;
plot(model_2_nn_8)

Yapay sinir ağı modelimiz görüldüğü gibidir.
plotnet(model_2_nn_8)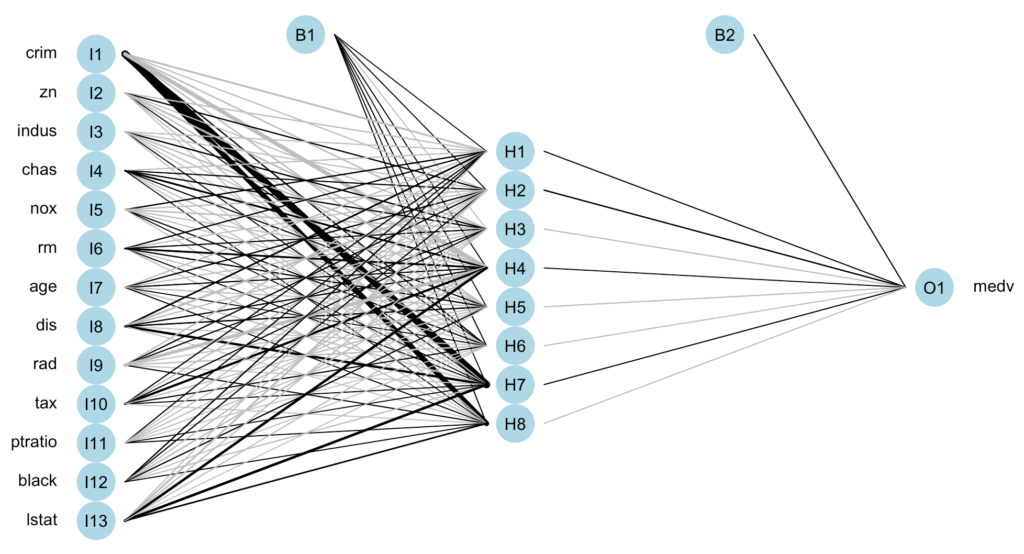
- modelimiz yani iki gizli katmandan oluşan modelimiz için üretilen hata değeri için bu kodu kullanabiliriz.
pr.nn1 <- compute(model_1_nn_5_3,test_verisi[,1:13])
pr.nn1 <- pr.nn1$net.result*(max(veri$medv)-min(veri$medv))+min(veri$medv)
test.cv.r1 <- (test_verisi$medv)*(max(veri$medv)-min(veri$medv))+min(veri$medv)
MSE1 <- sum((test.cv.r1 - pr.nn1)^2)/nrow(test_verisi)
print(MSE1)## [1] 0.007581668302- modelimiz için üretilen hata değeri;
pr.nn2 <- compute(model_2_nn_8,test_verisi[,1:13])
pr.nn2 <- pr.nn2$net.result*(max(veri$medv)-min(veri$medv))+min(veri$medv)
test.cv.r2 <- (test_verisi$medv)*(max(veri$medv)-min(veri$medv))+min(veri$medv)
MSE2 <- sum((test.cv.r2 - pr.nn2)^2)/nrow(test_verisi)
print(MSE2)## [1] 0.009965250114plot(test_verisi$medv,pr.nn1,col='red',main='2 Katmanlı - 1 Katmanlı Yapay Sinir Ağları',pch=18,cex=0.8)
points(test_verisi$medv,pr.nn2,col='blue',pch=16,cex=0.8)
abline(0,1,lwd=2)
legend('bottomright',legend=c('2 Katmanlı','1 Katmanlı'),pch=15,col=c('red','blue'))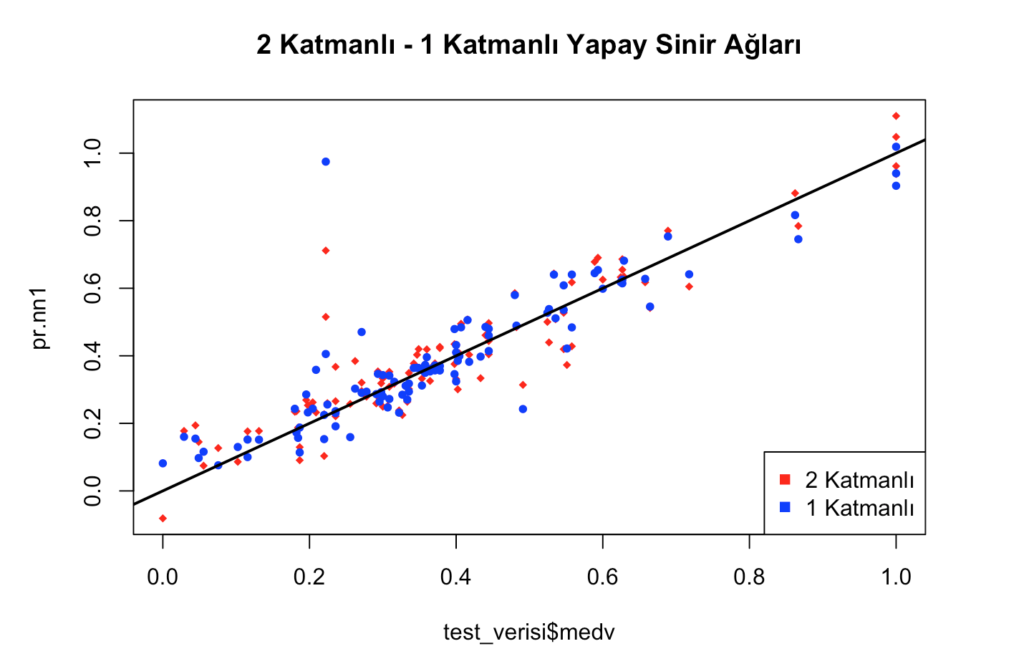
Garson Algoritması ile Parametre Önemi Belirleme
Bir sinir ağındaki değişkenleri bağlayan ağırlıklar, standart bir regresyon modelinde parametre katsayılarına kısmen benzerdir ve değişkenler arasındaki ilişkileri tanımlamak için kullanılabilir.
Ters etki bir yanıt değişkeniyle güçlü pozitif veya negatif ilişkilere sahip açıklayıcı değişkenlere verilen ağırlıklar için görülür. Bir sinir ağı ve bir regresyon modeli arasındaki bariz bir fark, eski durumda ağırlıkların sayısının fazla olmasıdır. Bu özellik, belirli değişkenlerin etkilerinin yorumlanmasının zor olmasına rağmen, doğrusal olmayan fonksiyonların çoklu etkileşimlerle modellenmesi için sinir ağlarını çok esnek kılması bakımından avantajlıdır.
Garson Algoritması, model ağırlıkların yapısını bozarak denetimli bir sinir ağındaki tek bir cevap değişkenleri için açıklayıcı değişkenlerin göreceli önemini tanımlar. Garson algoritması ile yapay sinir ağlarında parametrelerin önemi belirlenir.
Yanıt değişkeni için spesifik bir açıklayıcı değişkenin nispi önemi (veya birliğin gücü) ilgili düğümler arasındaki tüm ağırlıklı bağlantıların belirlenmesiyle belirlenebilir. Bağlantılar her giriş düğümü için aranır ve diğer tüm girişlere göre ölçeklenir. Modeldeki yanıt değişkeni ile ilişkiyi açıklayan her açıklayıcı değişken için tek bir değer elde edilmiştir.
Orijinal algoritma, sıfırın mutlak büyüklüğü olarak göreceli önemi gösterir ama yanıtın yönü belirlenemez. Garson Algoritması makine öğreniminin popüler olmasıyla daha da geliştirilerek pozitif ya da negatif yönünü tahmin etmemize olanak verir.
Algoritma sadece bir gizli katmanı ve bir bağımlı değişkenli kurulmuş sinir ağları modelleri için çalışır.
Daha detaylı bilgilere “help(”garson“)” fonksiyonu ile ulaşabilirsiniz.
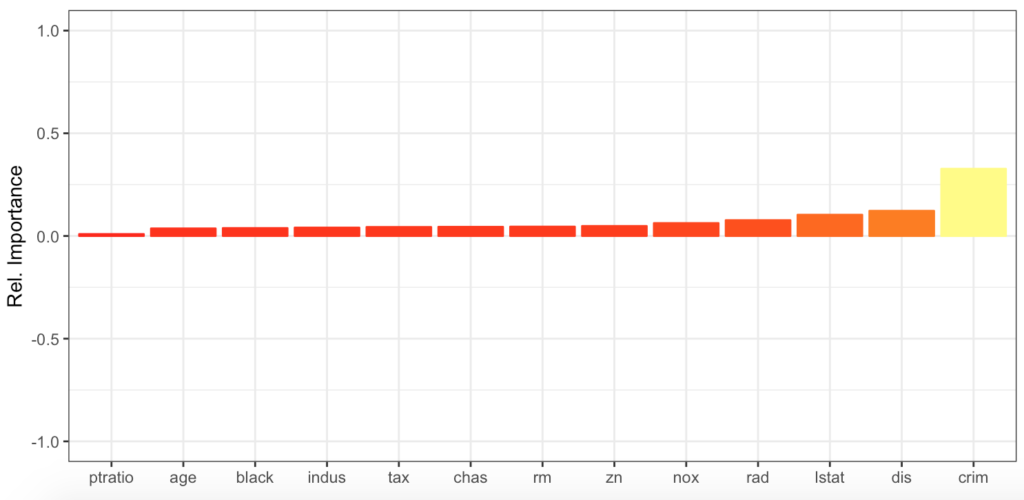
garson(model_2_nn_8)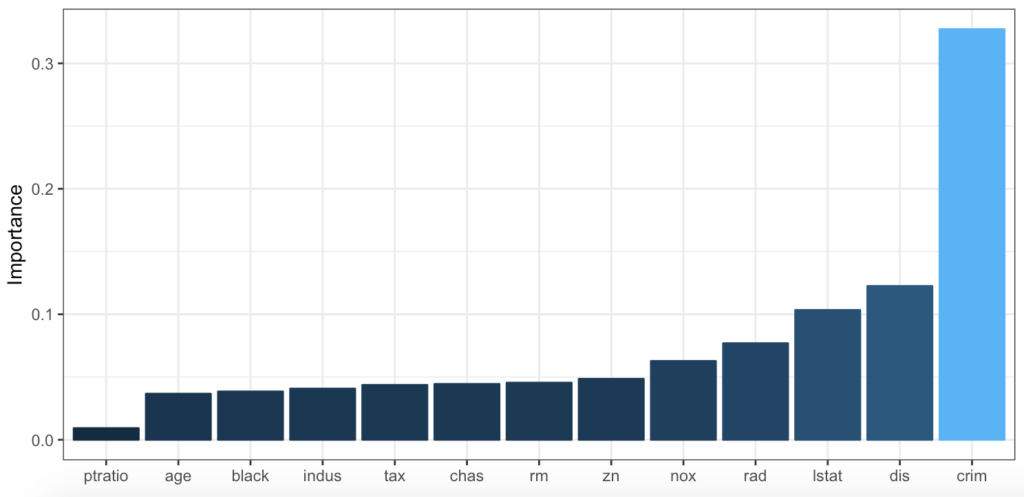
cols <- heat.colors(5)
garson(model_2_nn_8) +
scale_y_continuous('Rel. Importance', limits = c(-1, 1)) +
scale_fill_gradientn(colours = cols) +
scale_colour_gradientn(colours = cols)Bu grafiklerde bağımlı değişkeni etkileyecek en önemli parametleri önem sırası ve önem gücüne göre sıralı görebilmekteyiz.
Pozitif ve negatif kısmi önemi görmek için bakınız: https://www.r-bloggers.com/variable-importance-in-neural-networks/
Hassaslık Analizi Lek Profil
Lek’s Profil yöntemi ile yapay sinir ağlarında hassaslık ölçümü gerçekleştirilebilir.Profil metodu oldukça geneldir ve tahmin metodu ile R’deki herhangi bir istatistiksel modele genişletilebilir. Bununla birlikte, yapay sinir ağlarında duyarlılığı değerlendirmek için yaygın kullanılan birkaç yöntemden biridir.
Lek Profil yöntemi, açıklayıcı değişkenlerin etkisini, herbiri ayrı değişken için değerler aralığı boyunca tahmin edilen yanıtın bir grafiğini döndürerek değerlendirmek için kullanılabilir. Tüm açıklayıcı değişkenler, ortalama (veya başka bir sabit değer) olarak tutulurken, ilgili değişken, gözlem aralığındaki minimumdan maksimum değere dizilir ve matris oluşturulur. Bu matris (veya data frame) daha sonra takılan model nesnesindeki yanıt değişkeninin değerlerini tahmin etmek için kullanılır. Bu, tüm cevap eğrilerini elde etmek için her açıklayıcı değişken için tekrarlanır. Gruplar, derecelendirilmemiş açıklayıcı değişkenlerin sabit olarak tutulduğu değerleri, belirli kümelemeleri, kümelenmeye dayalı grup atamaları veya kullanıcı tarafından tanımlanan keyfi gruplandırma olarak tanımlar.
lekprofile(model_2_nn_8)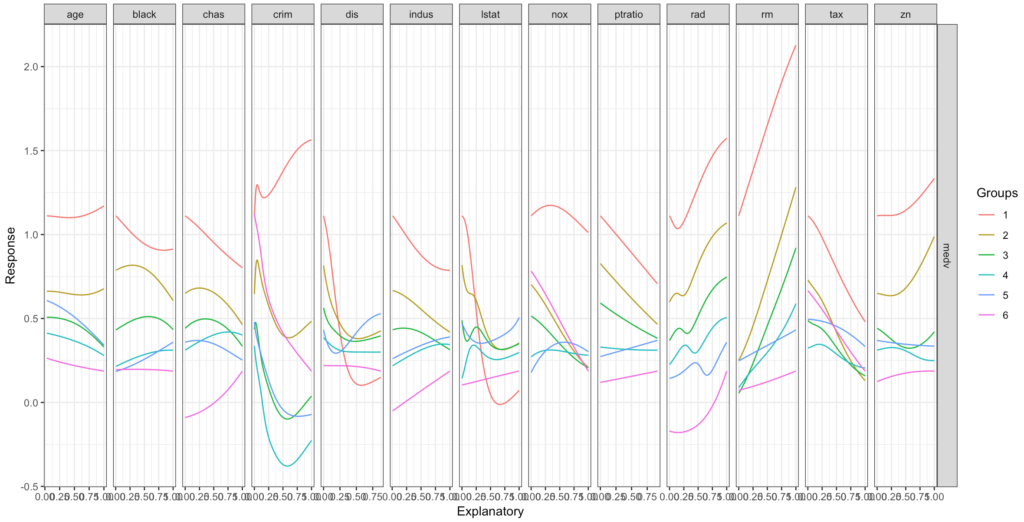
Grup sayısı, araştırmacı tarafından ayarlanabilir bunun için group_vals = fonksiyonu kullanılmalıdır.
lekprofile(model_2_nn_8, group_show = TRUE, group_vals = 4)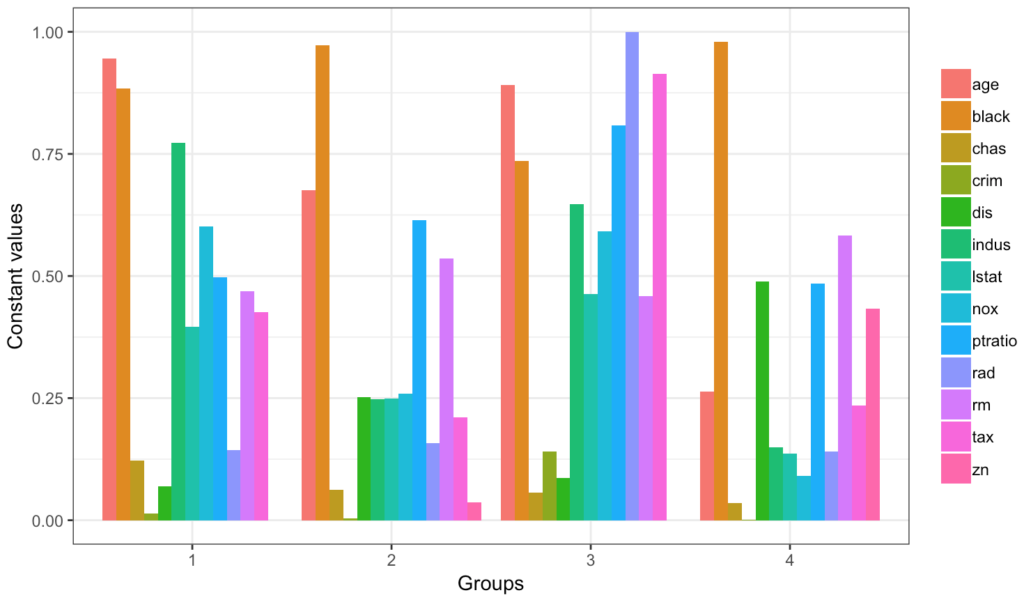
Daha detaylı bilgilere “help(”lekprofile“)” fonksiyonu ile ulaşabilirsiniz.
Unutulmamalıdır ki bu yöntemler sadece gizli katmanı olan yapay sinir ağları için kullanılabilir.
Farklı iterasyonlar ile sonuçları görelim
deneme_model <- train(medv~., data = egitim_verisi, method = "neuralnet", preProcess = c("center", "scale"), tuneLength = 10)
deneme_model## Neural Network
##
## 400 samples
## 13 predictor
##
## Pre-processing: centered (13), scaled (13)
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 400, 400, 400, 400, 400, 400, ...
## Resampling results across tuning parameters:
##
## layer1 RMSE Rsquared MAE
## 1 0.09987063155 0.7516664975 0.06806470397
## 3 0.10876532789 0.7274540827 0.07087553814
## 5 0.10834857036 0.7264177203 0.07261083063
## 7 0.11912874008 0.6785277332 0.07890164303
## 9 0.12946251617 0.6401327976 0.08397045343
## 11 0.14544843410 0.5761260689 0.09259361764
## 13 0.14366747433 0.5802165089 0.09528286449
## 15 0.14840205235 0.5853328755 0.09900929572
## 17 0.15872593449 0.5367323987 0.10579248706
## 19 0.17545248907 0.4972676827 0.11192100840
##
## Tuning parameter 'layer2' was held constant at a value of 0
##
## Tuning parameter 'layer3' was held constant at a value of 0
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were layer1 = 1, layer2 = 0 and
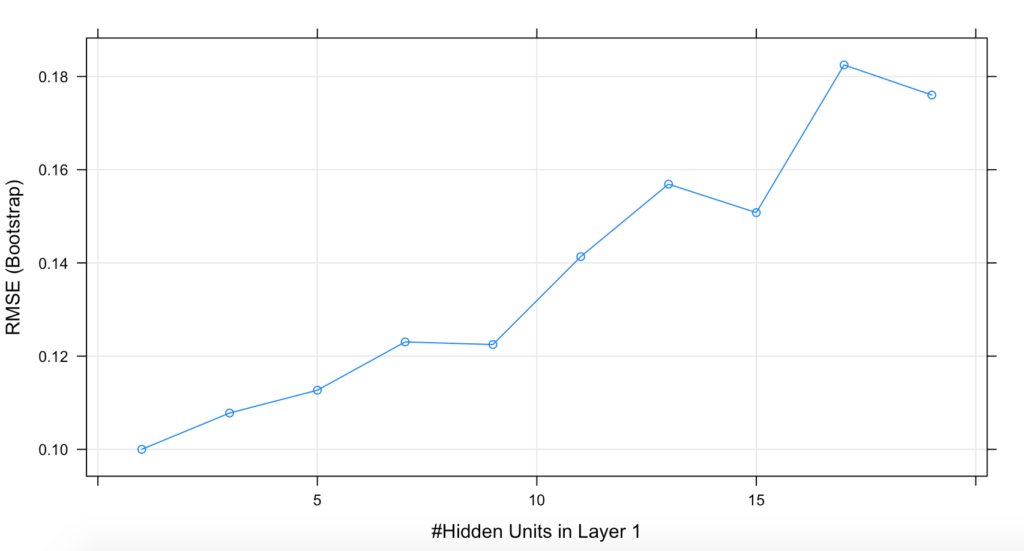
## layer3 = 0.plot(deneme_model)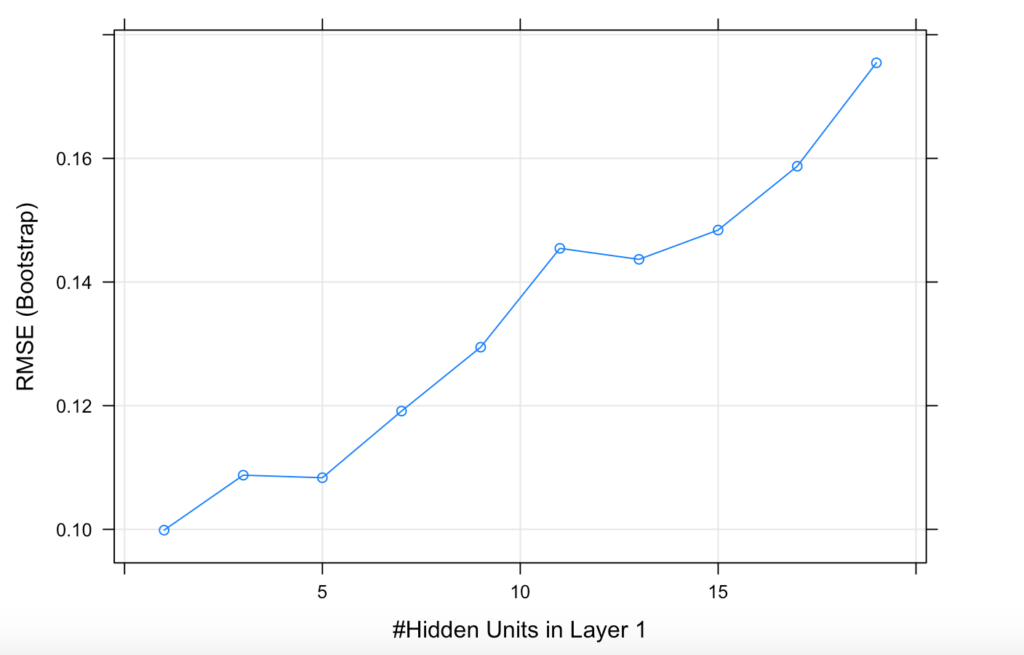
Çıktıdan ve grafikten de görüldüğü üzere gizli katman sayısı arttıkça ya da katmandaki nöron sayısı arttıkça hata artıyor. Final modelini oluşturmadan önce deneme yanılma yoluyla bu sonuçları elde edip değerlendirmek gerekiyor.
deneme_model_3 <- train(medv~ ., data = egitim_verisi, method = 'neuralnet', tuneGrid = expand.grid(layer1 = c(6), layer2 = 0, layer3 = 0))
deneme_model_3## Neural Network
##
## 400 samples
## 13 predictor
##
## No pre-processing
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 400, 400, 400, 400, 400, 400, ...
## Resampling results:
##
## RMSE Rsquared MAE
## 0.104029237 0.7652656017 0.06387888277
##
## Tuning parameter 'layer1' was held constant at a value of 6
##
## Tuning parameter 'layer2' was held constant at a value of 0
##
## Tuning parameter 'layer3' was held constant at a value of 0plot(deneme_model_2)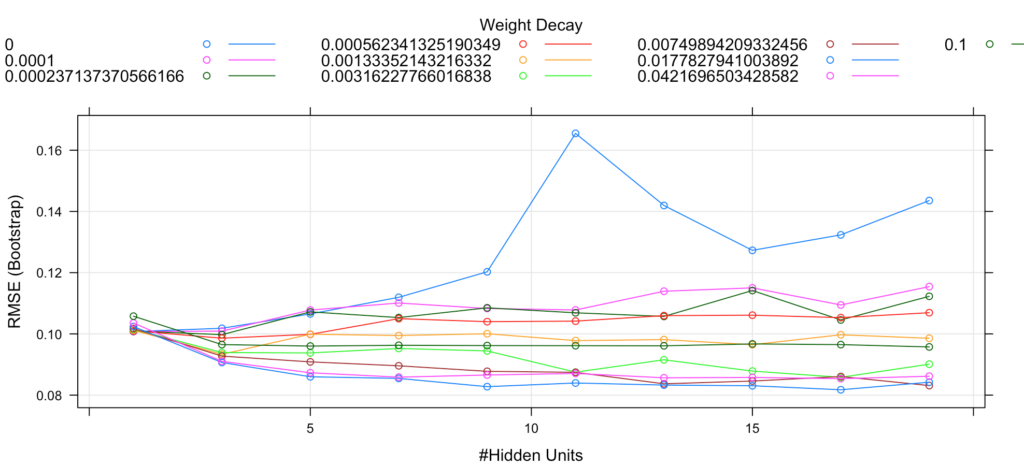
Bu işlemle “nnet” yöntemi yaptığı inteasyonları göstermektedir çıktıda, yaptığı her interasyonu göstererek her seferinde ağırlığı değiştirmektedir. Hatayı düşürerek her seferinde farklı ağırlıklar belirleyerek en optimal düzeye geldiğinde ise döndürmeyi bırakmaktadır. Bu grafikte ağırlıkların katmanlardaki hatalarını göstermektedir.
Yapay Sinir Ağları vs. Lineer Regresyon
Yapay sinir ağları, geleneksel yöntemlere alternatif olarak son yıllarda ciddi oranda kullanımı ve popülerliğini arttırmış durumdadır. Regresyonun varsayımları gibi varsayımlar barındırmayan yapay sinir ağları, makine öğrenmesi algoritmaları arasında özel bir yere sahiptir. Bunun sebebi yapıyı görebilmesi ve genelleştirme yapabiliyor olmasıdır. Her parametrenin etki gücünü kendi belirleyip, önemli olan parametrenin katsayısını arttırarak bağımlı değişken üzerindeki etkisi yükseltir.
Bu örnekte yapay sinir ağları ile geleneksel regresyon kıyaslaması yaparak hangisinin daha başarılı olacağı incelenecektir.
Cross Validation yapılacağı için regresyon modeli kurarken “glm()” fonksiyonunu tercih edilecektir çünkü lm() fonksiyonundan ziyade glm() fonksiyonu daha kullanışlı olacaktır.
lm.model <- glm(duzeltilmis_veri, data = egitim_verisi)summary(lm.model)##
## Call:
## glm(formula = duzeltilmis_veri, data = egitim_verisi)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.36196258 -0.06192274 -0.01188999 0.03422944 0.55375382
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.509693824 0.058441037 8.72151 < 0.000000000000000222 ***
## crim -0.176554304 0.076392072 -2.31116 0.0213502 *
## zn 0.094166497 0.035375762 2.66189 0.0080949 **
## indus 0.039022412 0.042402330 0.92029 0.3579963
## chas 0.067770006 0.023017488 2.94428 0.0034329 **
## nox -0.214598778 0.047285518 -4.53836 0.000007583327756633 ***
## rm 0.423881935 0.053930825 7.85973 0.000000000000038768 ***
## age 0.001766822 0.032952093 0.05362 0.9572673
## dis -0.389511872 0.057705368 -6.75001 0.000000000054381744 ***
## rad 0.177289803 0.038472525 4.60822 0.000005526755906364 ***
## tax -0.161042991 0.049349338 -3.26333 0.0011993 **
## ptratio -0.205511181 0.031994399 -6.42335 0.000000000392559968 ***
## black 0.080283487 0.027770361 2.89098 0.0040576 **
## lstat -0.455741706 0.047932261 -9.50804 < 0.000000000000000222 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 0.01150500681)
##
## Null deviance: 16.4254219 on 399 degrees of freedom
## Residual deviance: 4.4409326 on 386 degrees of freedom
## AIC: -635.08923
##
## Number of Fisher Scoring iterations: 2lm.pred <- predict(lm.model, test_verisi)
MSE.lm <- sum((lm.pred - test_verisi$medv)^2)/nrow(test_verisi)Lineer modelimizde ki hata değerimiz;
MSE.lm## [1] 0.01022269154Görselleştirdiğimizde
par(mfrow=c(1,2))
plot(test_verisi$medv,pr.nn1,col='red',main='Gerçek - Tahmin (Yapay Sinir Ağları)',pch=18,cex=0.7)
abline(0,1,lwd=2)
legend('bottomright',legend='NN',pch=18,col='red', bty='n')
plot(test_verisi$medv,lm.pred,col='blue',main='Gerçek - Tahmin (Regresyon)',pch=18, cex=0.7)
abline(0,1,lwd=2)
legend('bottomright',legend='LM',pch=18,col='blue', bty='n', cex=.95)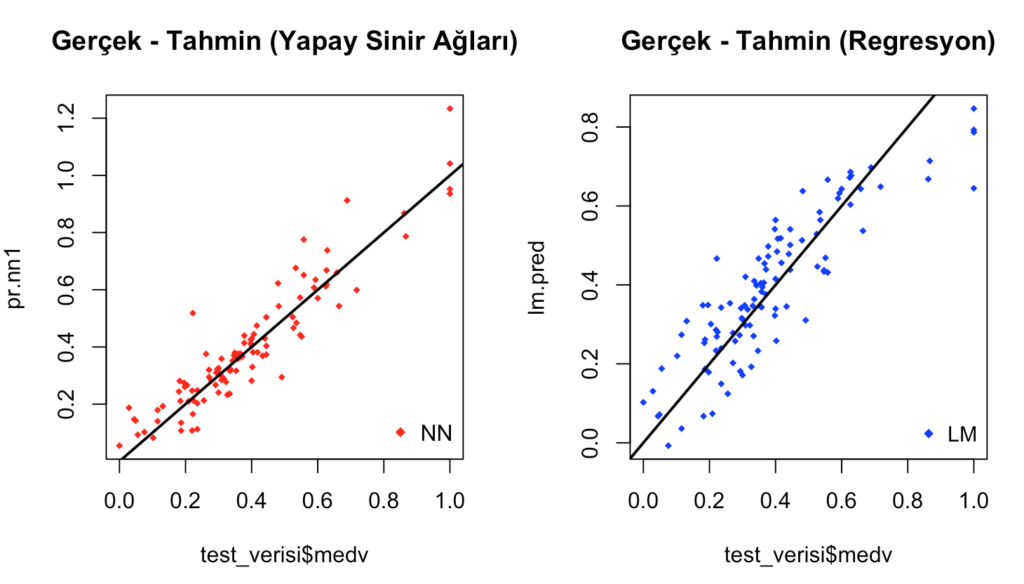
Grafikte yapay sinir ağları modeli ve regresyon modelinin grafiğini görülmektedir.
Aynı grafik üzerinde görmek istediğimizde,
plot(test_verisi$medv,pr.nn1,col='red',main='Gerçek - Tahmin (Yapay Sinir Ağları)',pch=18,cex=0.7)
points(test_verisi$medv,lm.pred,col='blue',pch=18,cex=0.7)
abline(0,1,lwd=2)
legend('bottomright',legend=c('YSA','LM'),pch=18,col=c('red','blue'))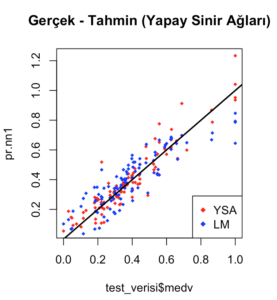
boxplot(lm.pred,xlab='MSE CV',col='cyan',
border='blue',names='CV error (MSE)',
main='Cross Validation MSE Regresyon Modeli',horizontal=TRUE)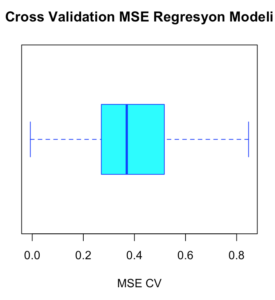
Olarak görülmüştür.
Yazımın sonuna gelirken yapay sinir ağlarının önemini tekrar belirtmek isterim. Günümüz teknolojilerinde aklımıza gelen hemen hemen hepsinde bir şekilde yapay sinir ağları gibi makine öğrenmesi algoritmaları kullanılmaktadır. Gelecek 10 yıl içinde adını duymadığımız meslekler, statüler ve lisasta bölümler olacaktır ama veri okur yazarlığı bilmeyen kişiler geleceği planlayanlar arasında olamayacak ve zamanla biteceklerdir.
Gelecekte verinin bize fısıldadığı cümleleri anlayamayan, verinin karakterini algılayamayan kişiler ya da meslek grupları bitecek veya olduğu yerde kalacaktır. O yüzden veri okur yazarlığı konusunda kendimizi hep geliştirme çabası içinde olmalıyız.
Varsayımlarınızın sağlanması dileğiyle,
Veri ile kalın, Hoşça kalın.
Kaynak: U.K.Çınar,(2018), R programıyla Yapay Sinir Ağları ile Zaman Serisi Modellemesi
Kaynak: https://rpubs.com/julianhatwell/annr
Kaynak: https://www.r-bloggers.com/fitting-a-neural-network-in-r-neuralnet-package/
Kaynak: https://ekblc.files.wordpress.com/2014/02/ysa.pdf
Görselin kaynağı: www.psikolojik.gen.tr , www.mesutpek.com
Related Posts:
- DocLing: Yapay Zekada Belgelerle Çalışmak
- Yapay Zeka Mühendisliğinin (AI Engineering) Yükselişi
- Gerçekçi Bir Yapay Zeka Mühendisi (AI Engineer) Yol Haritası
- Yapay Zeka ve Demokrasinin Gizli Krizi: Orta Sınıfın…
- Veri Kalitesi ve Yapay Zeka: Veri Mühendisliğinin Önemi
- A2A Protokolü: Yapay Zeka Ajanlarının İşbirliğinde…
10 Responses
Bir yanıt yazın Yanıtı iptal et
Yorum yapabilmek için oturum açmalısınız.


Bilgilendirici olmuş.
Elinize sağlık
Teşekkürler
Merhaba Hatice Hanım,
Umarım faydalı olmuştur.
Saygılar
Merhaba,
İçerik oldukça iyi ama garson fonksiyonu R da çıkmıyor. bunun nedeni nedir?
Emeğinize sağlık güzel bir çalışma olmuş
Merhaba Eda Hanım,
Çok teşekkür ederim.
merhaba, öncelikli olarak paylaşımınız için teşekkürler.
duzeltilmis_veri <- parametre_birlestirme("medv", Boston)
ilk başka veri <- Boston ile bu veriyi aktarmışken bu kod satırında neden "veri" kullanılmadı. boston verisi dışında bir csv dosyası ile çalışıyorsak ne yapmalıyız? yardımcı olabilirseniz çok memnun olurum. teşekkürler
Şengül Hanım merhabalar,
Sorunuzu tam olarak anlayamadım hocam. Aldığınız hata sanırım Boston verisi bulunamadı olabilir. Kullandığımız kütüphane değişmiş ya da bir güncelleme gelmiş olabilir. Başka bir veriyle bu çalışmaları kolaylıkla yapabilirsiniz. Gerekli manipülasyonları dönüşümleri hatasız yaptığınızdan emin olun. Eğer sorunuz devam ederse linkedin üzerinden bana ulaşın lütfen.
Merhaba, öncelikle yardımlarınız için teşekkürler. Kaynakçaya ekleme içi “Kaynak: U.K.Çınar,(2018), R programıyla Yapay Sinir Ağları ile Zaman Serisi Modellemesi” belirttiğiniz içeriği mi kullanmalıyım?
Merhaba Şengül Hanım,
Umarım faydalı olmuştur. Kaynak için hangi türde kaynak vereceğinize göre değişir. APA formatında mı vereceksiniz bilemiyorum. Genelde online kaynakçalar şu şekilde veriyor. “CINAR. U.K, (2018), “sayfanın linki”, Erişim Tarihi:xx-xx-20xx” Arzu ederseniz bu şekilde belirtebilirsiniz. Eğer hakemli bir dergiye gönderecekseniz belirli formatları vardır zaten. Ona göre uyarlayabilirsiniz.
Saygılarımla
Tamamdır bilgi için teşekkürler. Hocam birde geri beslemeli yapay sinir ağı ile tahmin işlemi yapılamıyor mu? Yapılabiliyorsa geri beslemeli bir ağ için örnek kod bloku paylaşabilir misiniz?