![]()
Survival Analysis and Kaplan Meier Method in R
Utku Kubilay ÇINAR
Sağkalım analizi; konu olan bir olayın, gerçekleşme süresine kadar üretilen verilerin analiz edilmesidir. Bir örnekle açıklanacak olursa, ölümcül bir hastalığa yakalanan bir hastanın, hastalık süresince kullandığı ilaçların, hastanın bünyesinde oluşturduğu etkiler (sadece ilacın etkileri değil, hastanın yaptığı her davranış, olay, tanımlayıcı durumlar. Her şey olabilir.) veri olarak düşünüldüğünde, bu etkilerin (verilerin) analiz edilmesine, sağkalım analizi denilmektedir. Bu olay sadece hastanın ölümü ile sonuçlanmayabilir, örneğin hasta iyileşme sürecinde ürettiği veriler de bu analize örnek olabilir.
Hastalıktan örnek verdiğim için bu analizlerin sadece tıp ve medikal alanlarda kullanıldığını düşünmeyin. Ekonomi, bir makinanın bozulması, e-ticaret ve sosyal yaşam gibi birçok alanda da kullanılmaktadır. Ekonomik alandan örnek verecek olursam, bir şirket aynı şartlar altında, aynı koşullarda ya da aynı yatırım miktarlarıyla daha ne kadar varlığını devam ettireceğinin hesabı (weibull dağılımı gösterir), sağkalım analizleri ile hesaplanmaktadır.
Kısaca Sağkalım Analizleri, ilgilenilen bir olayın, olmasına kadar geçen sürede üretilen verilerin analiz edilip yorumlanmasıdır. Bu analizlerde de parametrik olmayan yöntemler kullanılmaktadır.
Sağkalım Analizleri, 1958 yılında Kaplan ve Meier tarafından 1958 yılında geliştirilmiştir ve bu konu üzerine çalışan Cox ise “Oransal Hazard Modeli”ni geliştirmiştir (İnceoğlu, F., 2013).
Sansürlü Veri
Kısaca, sağkalım süresi tam olarak bilinemeyen vakalar sansürlü (censored) olarak adlandırılır.
Sağkalım analizlerinde, veriler çoğunlukla sansürlü veriden oluşmaktadır. Sansürlü veriler sağdan sansürlü veri ve soldan sansürlü veri olmak üzere ikiye ayrılır. Yine tıp alanından bir örnekle açıklamak gerekirse, ya hasta takipten çıkar (iyileşmiş olabilir, artık kontrollere gelmemiş olabilir) ya da hastalık dışından kaynaklanan bir sonuçla hasta ölmüş olabilir (hasta AIDS hastası olmuş olsun, bu sebeple AIDS ile ilgili analizler yapılıyordur fakat hasta trafik kazasından ölmüş) gibi örneklerle sağdan ve soldan sansürlü veriyi açıklayabiliriz.
Veri bilimcilerin ilgilendiği bir konudan örnekle açıklamak gerekirse, telekomünikasyon firmalarında çalışan meslektaşlarım, müşterilerin Churn olması üzerine bir analiz gerçekleştiriyor olsun. Churn olanların bazıları sadece hatları kapanmasın diye 3-4 ayda bir hatlarına para yatırıyor da olabilir (tam anlamıyla Churn değil), ya da başka bir operatör firmaya da geçmişte olabilir (ya da uzun süreli ülke dışına çıktığını düşünelim) ve biz bu iki durumu da bilmediğimizi varsayalım. Tek bildiğimiz uzun zamandır o müşterinin telekomünikasyon firmasına para kazandırmadığıdır ve veri bilimcinin o müşteriyi artık takip edemiyor olmasıdır (Sağkalım analizlerinde, bu duruma sistemden çıkma denir).
Sağkalım analizi ile farklı durumlar için elde edilen sağkalım oranları karşılaştırılmaktadır ve sağkalım sürelerini etkileyen açıklayıcı faktörler belirlenebilmektedir (Tuncay, A., 2005).
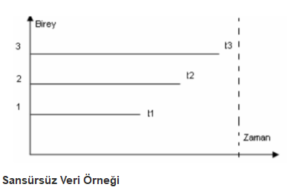
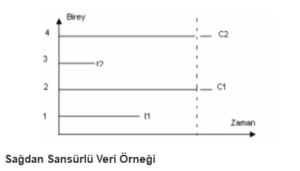
Grafikte her birey süreç içinde ölmüştür yani tarihler biliniyor ve başarısızlık durumu kesindir (Nelson, W., 1982).
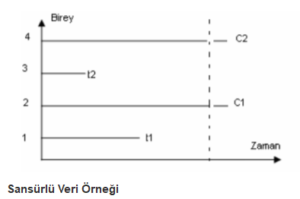
Bu grafiğe bakarsak 1. ve 3. bireylerde belirlenen zaman aralığında ölüm olayı gerçekleşmiştir. Ama 2. ve 4. bireyler belirlenmiş sağkalım süresinin sonunda hala yaşamaya devam etmektedir (İnceoğlu, F., 2013).
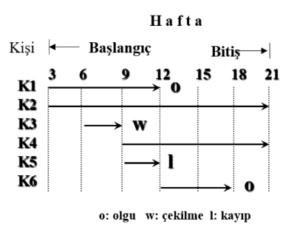
- Birinci kişinin başlangıçtan itibaren 12 hafta izlendiğini, 12. hafta sonunda olgu gözlendiğini ve sağkalım süresinin 12 hafta olduğu görülmektedir.
- İkinci kişinin başlangıçtan bitişe kadar izlendiğini, olgu gözlenmediğini ve sağkalım süresinin en az 21 hafta olmak üzere sansürlü olduğu görülmektedir..
- Kaynak: http://content.lms.sabis.sakarya.edu.tr/Uploads/54849/46733/ders_12_ya%C5%9Fam_analizleri.pdf
Sağdan Sansürlü Veri
Sağkalım süresi içinde, ilgilenilen nedenden değil de başka bir nedenden ölmüşse bu veriye sağdan sansürlü veri olarak isimlendirilir (AIDS olan birinin trafik kazasından ölmesi örneği). Sağdan sansürlü sağkalım zamanı, gerçek zamandan daha kısadır (t < c).
Soldan Sansürlü Veri
Gerçek sağkalım zamanı araştırmacı tarafından belirlenmiş zamandan daha az ise veriler soldan sansürlü veridir (t>c). Sağkalım analizlerinde veriler genellikle sağdan sansürlüdür.
Kaplan – Meier Yöntemi
Bu yöntemde zaman süresi önemlidir. Unutulmamalıdır ki Kaplan-Meier Yöntemi, analiz değil bir şekildir, sağkalım eğrilerinin genel adıdır. Bu eğrilerin karşılaştırılmasında ise Log-Rank Testi kullanılır . Kaplan-Meiser Yöntemi’nde her olay için bir olasılık tahmin edilir. Bu değerler bir grafiğe döküldüğünde basamak gibi görünür.
Yaşam tablosu yönteminden farklı olarak, her ölüm zamanını ayrıca değerlendirmesi nedeniyle, Kaplan-Meier yönteminde sağkalım olasılıkları, adımsal (step) fonksiyon biçiminde belirir. Bir önceki (ölüm) kestirim anından sonra, yeni ölüm zamanına dek, başka ölüm olmaması nedeni ile olasılık değişmez kalmaktadır ve grafiksel gösterimde bir merdiven görüntüsü ortaya çıkmaktadır (Şenocak, M.) .
Kaplan – Meier Yönteminin Varsayımları
- Deneklerin çalışmaya katıldığı tarih bilinmelidir.
- Olayın ortaya çıktığı tarih (zamanı, periyodu) bilinmelidir.
- Kayıpların (sansürlerin) ortaya çıktığı tarih bilinmelidir.
- Olayın ve kayıpların aynı anda ortaya çıkmaması gerekmektedir. (Erkorkmaz, Ü.)
Uygulama
Veri setini buradan indirebilirsiniz.
İş bulamayan ya da bulan kişilerin bulunduğu veri setinde; kişilerin özellikleri ile beraber Sağkalım Analizlerinde kullanacağımız değişkenler de vardır. Bunlardan bazıları, 5 olayla beraber iş bulup-bulmamasına göre 0 ve 1 değerleri, tarih (periyot) ve kişilerin bulundukları gruplardır. Bazı kişiler 5 olayın bir iki tanesine katılmışken bazıları iş bulup diğer olaylara katılmamıştır (sağdan ve soldan sansürlü olarak düşünebilirsiniz).
Öncelikle veri setini yükleyelim ve gerekli kütüphaneleri çağıralım.

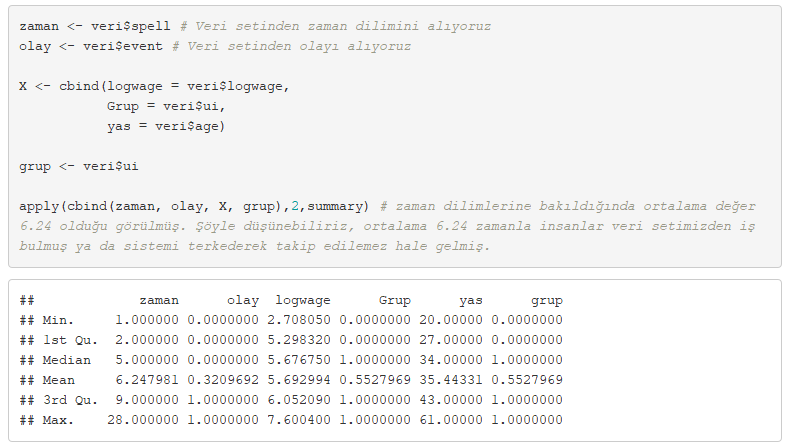
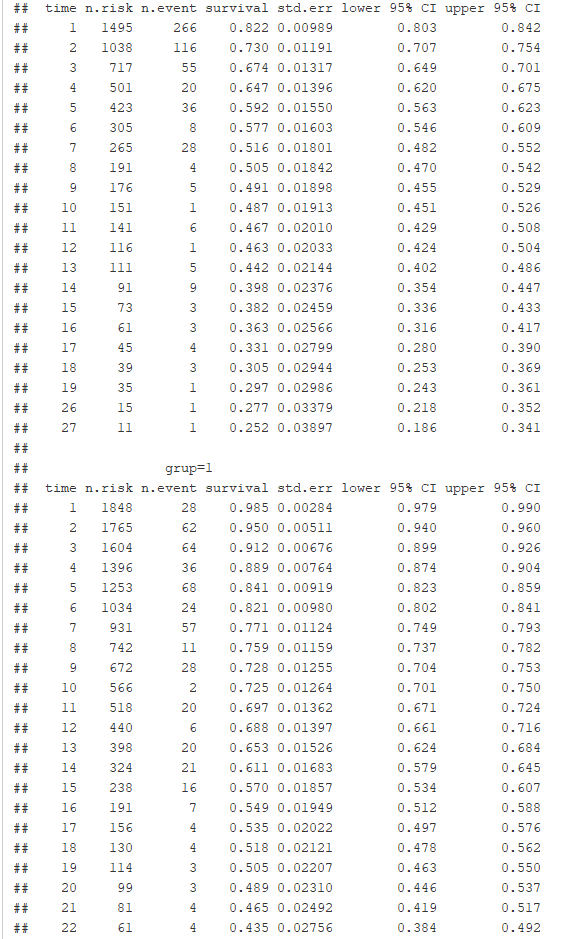
Kullanacağımız verileri ayrıştıralım ve özet istatistiklerini inceleyelim.
Kaplan – Meier Görseli (Sağkalım Fonksiyonu)
Kaplan-Meier Yöntemi’nin bir görsel şekil olduğunu ve basamağa benzediğini daha önce belirtmiştim. Şimdi Kaplan-Meier Yöntemini uygulayalım ve olasılıkları görelim.
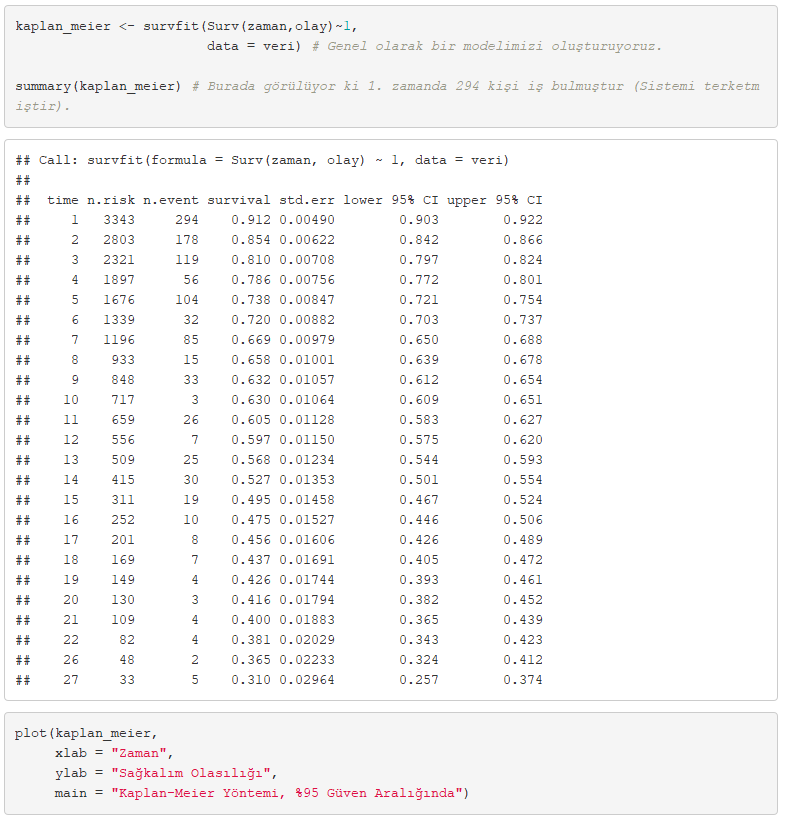
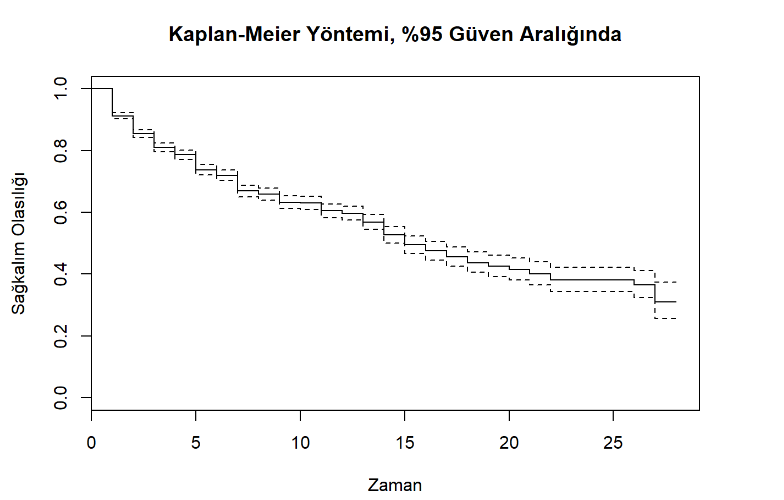
Grafikte görüldüğü üzere olasılıklar basamak gibi merdiven şeklinde oluşmuştur.
Kaplan – Meier Görseli-Gruplar Bazında
Daha önce “ui” grubuna göre böldüğümüz veriyi gruplar bazında inceleyelim. Böylelikle hangi grubun daha iyi olduğunu görmüş olacağız. Bu kararı vermek için ise Log-Rank Testini kullanacağız.

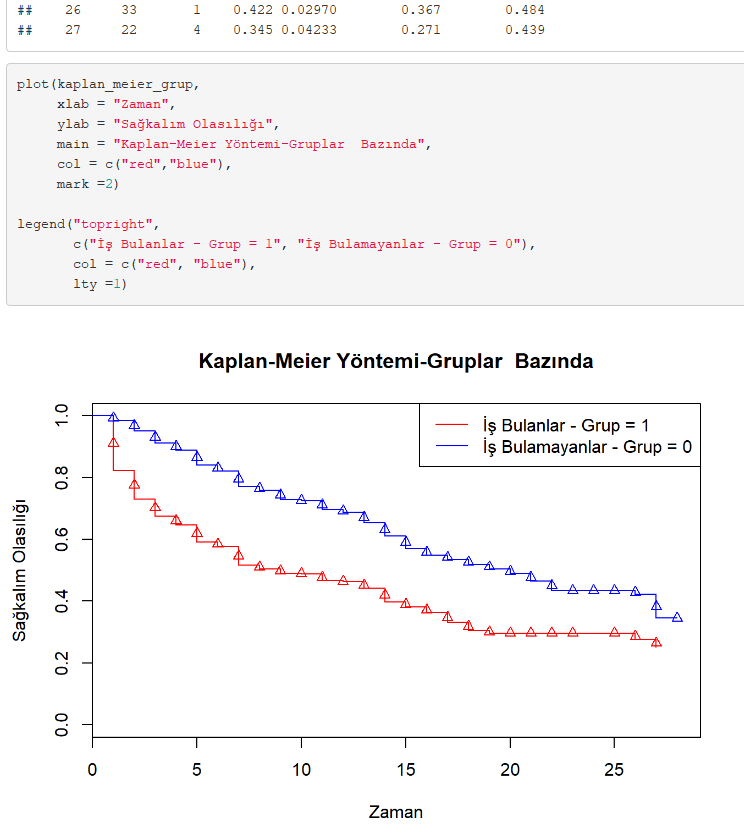
Görselde gördüğümüz iki çizgi, iş bulanlar ve bulamayanlardır yani sıfır ve birler için üretilen “Sağkalım Olasılıklarıdır”.

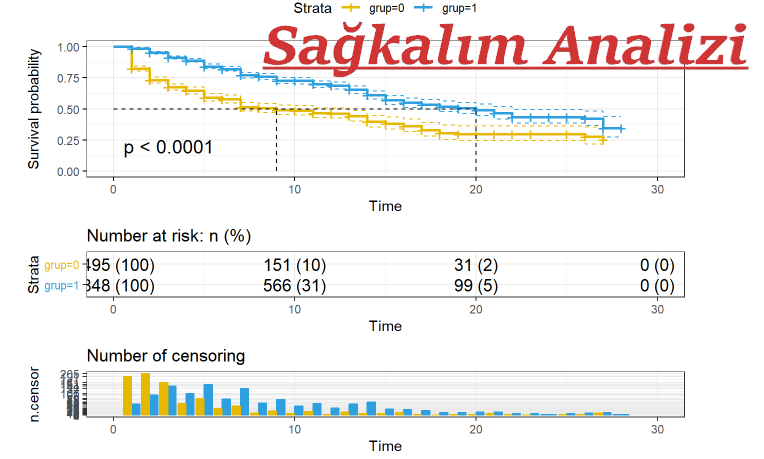
Eğrilerdeki dikey işaret, bir hastanın şu anda sansür edildiği anlamına gelir (bknz: Kaplan – Meier Geometrik yorumu). Sıfır zamanında, hayatta kalma olasılığı 1’dir (veya katılımcıların % 100’ü hayatta). 20. zamanda hayatta kalma olasılığı gruplar için 0.50 (1. grup için) ve 0.25 (0. grup için).
Sağkalım Olasılığı grafiğindeki çizgiler ise ortanca(medyan) değerlerini verir. 0. grup(iş bulanlar) için medyan değeri yaklaşık 9. gün iken, 1. grubun((iş bulamayanlar) medyan değeri 20. gün olduğu görülmüştür. Bu tabloya bakıldığında 0. grup üyeleri sistemi daha hızlı terk ediyor, daha iyi bir grup oldukları söylenebilir.
Log – Rank Testi
“Gözlemlere atanan wi skor değerlerinde dayanmaktadır. Skorlar sağkalım fonksiyonlarının logaritmik fonksiyonudur. Altshuler’in tahminlediği logaritmik sağkalım fonksiyonu;
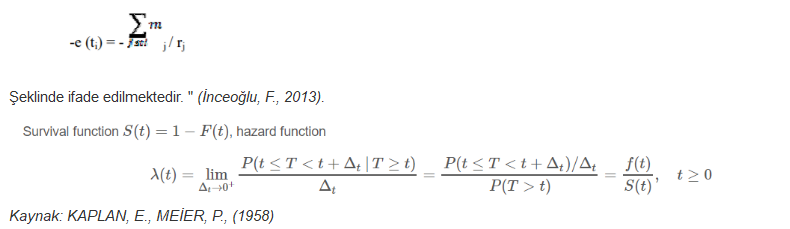
Sağkalım analizlerinde Log-Rank Testi ile iki grup arasında anlamlı bir farkın olup olmadığını görebiliyoruz. Log-rank Testi, tüm takip süresi boyunca gözlemleri eşit olarak ağırlıklandırır ve gruplar arasında hayatta kalma sürelerini karşılaştırmanın en yaygın yoludur. Log-Rank testi parametrik olmayan bir testtir. Wilcoxon testlerine göre daha güçlüdür.
Log Rank istatistiği, yaklaşık olarak Ki-Kare dağılımı gösterir. Bu sebeple Ki-Kare tablosu değerleri üzerinden kritik nokta değerleri belirlenir.
- Ho: %95 güven aralığında istatistiksel olarak iki grup arasında anlamlı bir fark yoktur.
- H1: %95 güven aralığında istatistiksel olarak iki grup arasında anlamlı bir fark vardır.

Hayatta kalım analizi, ilgilenilen sonuç değişkeninin, bir olay meydana gelene kadar geçen sürede üretilen verilerin analizi olduğu için bir dizi istatistiksel yaklaşımdır. Sağkalım fonksiyonu, bir bireyin (ya da örneğin) t zamanından ötesindeki bir zamana kadar hayatta kalma olasılığını temsil eder. Bu tahmin işleminde genellikle Kaplan – Meier yöntemi kullanılır. Lag-Rank Testi ise gruplar arasında istatistiksel olarak anlamlı bir farkın olup olmadığını belirler.
Varsayımlarınızın sağlanması dileğiyle,
Veri ile kalın, Hoşça kalın..
KAYNAKÇA:
- ERKORKMAZ, Ü., “Sağkalım (Yaşam) Çözümlemesi”, Sakarya Üniversitesi.
- http://content.lms.sabis.sakarya.edu.tr/Uploads/54849/46733/ders_12_ya%C5%9Fam_analizleri.pdf
- http://www.sthda.com/
- http://www.sthda.com/english/wiki/survival-analysis-basics
- İNCEOĞLU, F., (2013), “Sağkalım Analiz Yöntemleri ve Karaciğer Nakli Verileri İle Bir Uygulama”, İnönü Üniversitesi, Yüksek Lisans Tezi.
- KAPLAN, E., MEİER, P., (1958), “Nonparametric estimation from incomplete observations”.
- KATCHOVA, A., (2013), “Survival Analsis in R”.
- NELSON, W., (1982), “Applied Life Data Analysis”, New York, syf:584.
- ŞENOCAK, M., “Sağkalım Çözümlemesi İlkeleri”. Bknz: http://www.ctf.istanbul.edu.tr/dergi/online/1999v30/s4/994s1.htm
- TUNCAY, A., (2005), “Sağkalım Analizinde Parametre Tahmini Test İstatistikleri ve Bir Uygulama”, Ondokuz Mayıs Üniversitesi, Yüksek Lisans Tezi.
- YAYLA, M., E., (2013), “Yaşam Analizleri ve Cox Regresyon Modeli”.