Regresyon Modeli Kurmak

Erkan ŞİRİN 13 Haziran 2017 Makine Öğrenmesi 0 6443 884 kelime - 6 dakika86

---

Bu yazıya puan ver

(4 votes, average: 2,50 out of 5)

Loading...

---

Lineer regresyonun bazı varsayımları var:

1. Doğrusallık (linearity)

2. Eşvaryanslık (homoscedasticity)

3. Çok değişkenli normallik (multivariate normality)

4. Hataların bağımsızlığı (independence of errors)

5. Çoklu bağlantı yokluğu (multicollinearity)

Bir lineer model kurmadan önce yukarıdaki varsayımların karşılandığını kontrol etmek gerekir.

Regresyon Modeli Kurmak

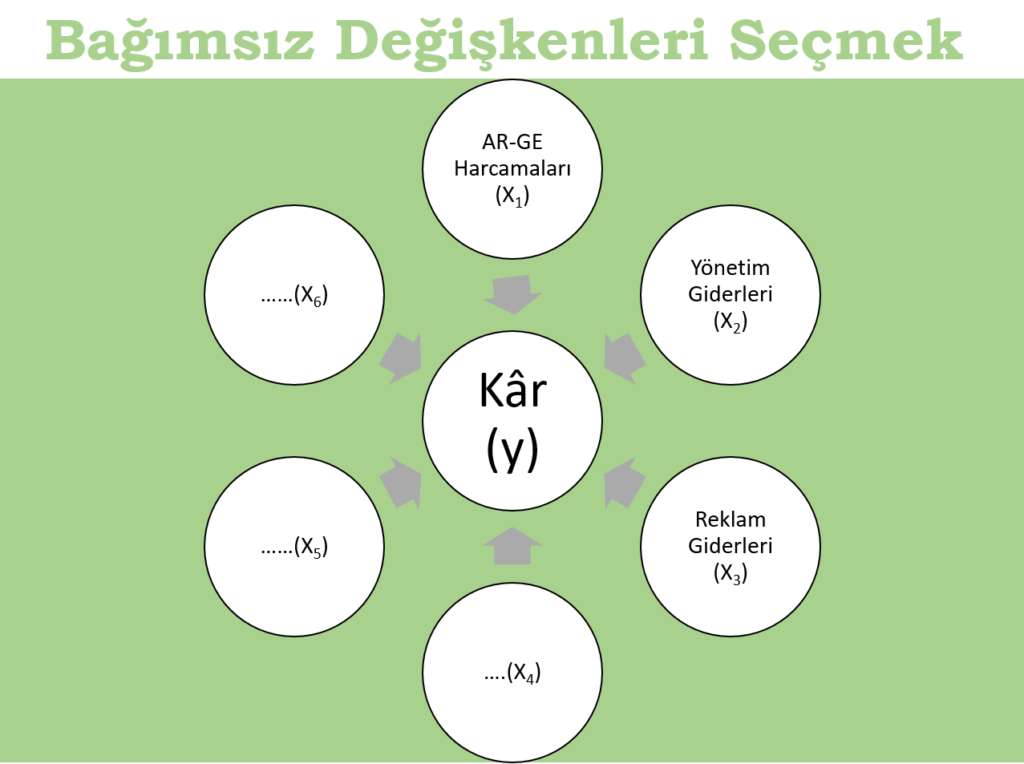
Lineer modelde iki farklı değişkenimiz vardı: ilki bağımlı değişken (hedef değişken – y) diğeri ise bağımsız değişken(ler)(predictors – x). Gerçek hayatta bir hedef değişkene etki eden birçok belirleyici değişken vardır. Örnek olarak şirket karı hedef değişken olsun. Karı etkileyen birçok faktör vardır. Peki biz kardaki değişkenliği açıklamak için bu faktörlerden hangilerini modelimize dahil edeceğiz? Hepsini mi? Kabaca seçtiğimiz 3-5 tanesini mi? En iyi sonucu vereni mi? En iyi sonucu hangisi verir? Bunu nasıl ölçeriz?

Yukarıda şekilde görüldüğü gibi AR-GE, yönetim giderleri, reklam giderleri gibi değişkenlerle birlikte hedef değişkene (kâr) etki eden daha birçok değişken (X_i) bulmak mümkündür. Ancak her bağımsız değişkeni modele dahil edersek model arap saçına dönebilir ve modelin anlaşılırlığı azalabilir. Peki bu karmaşaya nasıl bir çözüm bulunabilir? Yaygın olarak kullanılan beş yöntem ile bağımsız değişkenleri eleyerek sağlıklı modeller oluşturabiliyoruz.

Regresyon Model Kurmak için Beş Yöntem

1. Bağımsız değişkenlerin hepsini birden modele dahil etmek (All-in)

2. Geriye doğru eleme (Backward Elimination)

3. İleriye doğru seçme (Forward Selection):

4. İki yönlü eleyerek seçme (Bidirectional Elimination)

5. Sonuçları karşılaştırma (Score comparision)

Bunlardan 2, 3 ve 4 adım adım gerçekleştirilen yöntemlerdir. İlk yöntem olan hepsini birden modele dahil et yöntemini kuramlara dayalı geliştirilen modellerde kullanırız. Daha önce benzer alanda bir çok ampirik çalışma yapılmıştır ve bazı kavramlar arasındaki ilişkiler defalarca farklı örneklem üzerinde kanıtlanmıştır. Yani modele dahil edilen bağımsız değişkenlerin bağımlı değişkene etki ettiğine dair yeterince kanıt vardır. Ya da bu değişkenler size verilmiştir siz de ister istemez bunları modele koyacaksınızdır. Modelden değişken kaçırmak birilerinin istemediği sonuçların ortaya çıkmasını örtbas etmek gibi bir davranış olabilir diye ne verdilerse modele dahil edersiniz abi. Ne acayip bir gerekçe oldu yahu 🙂

Geriye doğru eleme yönteminde adımlar;

1. 1. Anlamlılık düzeyi belirlenir. Mesela; p < 0.05.

1. 1. Bir önceki yöntemde olduğu gibi tüm değişkenler modele dahil edilir.

1. 1. Her bir bağımsız değişkenin anlamlılık düzeyi incelenir. Eğer anlamlılık düzeyi model için belirlenenden daha büyük ise bu bağımsız değişken modelden çıkarılır. Eğer birden fazla var ise bu işlem en büyük p değerine sahip olana uygulanır. Şayet bütün p değerleri sınır değerden küçük ise model tamam demektir.

1. 1. Çıkarılan her bir değişkenden sonra model tekrar kurulur (eğitilir) ve üçüncü adım tekrar edilir.

1. Tüm bağımsız değişkenlerin p değeri eşik altında kalana kadar, başka bir deyişle bağımsız değişken ile ilişkisi istatistiksel anlamlı olana kadar üç ve dört tekrar edilir.

İleri doğru seçme yönteminde adımlar;

1. Anlamlılık düzeyi belirlenir.

2. Bağımlı değişken (y) ile tüm bağımsız değişkenler (X) tek tek basit regresyona sokulur. Aralarından en düşük p değerine sahip olan seçilir.

3. Bu en düşük değerli bağımsız değişken ile diğer bağımsız değişkenlerden oluşturulan modeller ayrı ayrı ikili olarak çoklu regresyona sokulur. En düşük p değerine sahip olan ikili seçilir.

4. En düşük p değerli ikili ile kalan bağımsız değişkenlerden üçlü kombinasyonlar oluşturulur ve modeller tek tek regresyona sokulur. p değeri anlamsız çıkana kadar üçüncü ve dördüncü adımlar tekrarlanır.

İki yönlü eleyerek seçme yönteminde adımlar;

1. Anlamlılık düzeyi belirlenir.

2. İleri doğru seçme yönteminde olduğu gibi anlamlılık düzeyi altında kaldığı sürece modele yeni değişkenler ilave edilir.

3. Geriye doğru eleme yönteminin tüm adımları uygulanır.

4. Yeni bir değişken ekleyemeyene ve eski değişkenlerden birini çıkaramayana kadar adım 2 ve 3 tekrarlanır.

Sonuçları karşılaştırma yönteminde adımlar;

1. Uyum indeksi için kriter belirlenir.

2. Olası tüm modeller denenir.

3. En iyi uyum indeksine sahip olan seçilir.

Bunlardan geriye doğru eleme yöntemi daha hızlı ve kullanılabilir olduğu için; hepsini birden modele dahil et yöntemi de kuramsal dayanağı olduğundan benim için daha kullanılabilir yöntemler.