R Kare ve Düzeltilmiş R Kare

Erkan ŞİRİN 11 Temmuz 2017 Doğrusal Regresyon, Model Değerlendirme, Regresyon, Teori 5 54501 910 kelime - 6 dakika196

---

Bu yazıya puan ver

(6 votes, average: 5,00 out of 5)

Loading...

---

Regresyon notlarımızda bahsettiğimiz gibi regresyon eğrisi temsil ettiği noktalara olabildiğince en yakından geçmeye çalışıyordu. Bunun için her bir noktanın eğriye olan uzaklığı hesaplanıyor ve toplam mesafeyi en küçük kılan doğru regresyon doğrusu oluyordu.

Yukarıda kazanç ve tecrübe arasındaki ilişkiyi gösteren bir grafik bulunuyor. Bu grafiğe göre tecrübe arttıkça kazanç da artıyor görünüyor. Grafiğe bakarak doğrusal regresyon formülümüzü şu şekilde yazabiliriz:
Kazanç = Sabit + β x Tecrübe

Kazanç hedef/bağımlı değişken (y), Tecrübe ise bağımsız değişken X. Yani burada tecrübeye dayanarak bir meslek erbabının kazancı tahmin edilmeye çalışıyor. Günlük hayattan edindiğimiz tecrübelere göre de bunu kolaylıkla anlayabiliriz. Avukat, doktor, danışman vb. bir meslek erbabı tecrübesi arttıkça daha fazla kazanmaktadır. Formüldeki Sabit ise hiç tecrübeli olmasa bile bu meslek erbabının belli bir kazanca sahip olduğunu gösterir.

Şimdi bu doğrunun noktalara en yakın bir doğrultuda geçmesi gerektiğini söylemiştik. Bunu sağlamak için noktaların doğruya olan uzaklığını hesaplıyoruz. Bu uzaklığın en az olduğu doğru, regresyon doğrusunu oluşturuyor. Bu uzaklığın minimum olmasını sağlayan yöntem ise en küçük kareler yöntemidir.

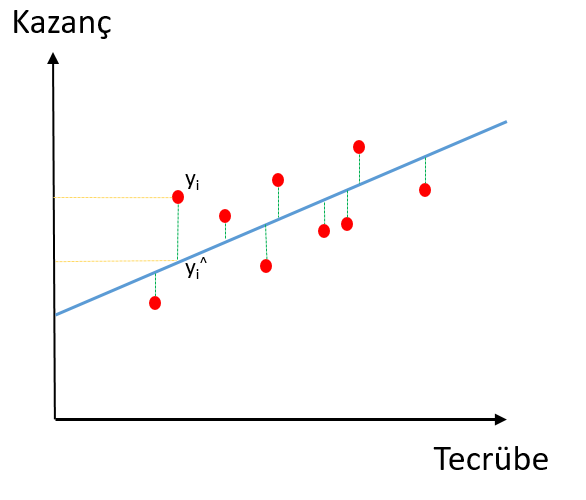
y_i değeri ile tahmin edilen y_i^{^} değeri arasındaki mesafelerin karelerinin toplamının en düşük olduğu eğri (doğru denklemi) regresyon eğrisidir. Burada işe karelerin karışmasının sebebi eksi değerlerden kurtulmaktır. Bunun başka bir yolu da mutlak değer almaktır. Doğruya isabet edemeyen her noktaya atık diyoruz. Aslında tüm noktalar doğru üzerine denk gelseydi mükemmel bir resgresyon eğrisi olacaktı ancak bu fiiliyatta pek mümkün olmaz. Bu nedenle eğriye denk gelmeyen her nokta bizim için atıktır (residual). Bu artıkların karelerinin toplamına Atıkların Karelerinin Toplamı (AKT) diyelim ve şöyle formülüze edelim:

Atıkların Kareler Toplamı (AKT) = TOPLAM(y_i – y_i^{^})²

Şimdi bir de her bir veri noktası acaba ortalamaya ne kadar uzaklıkta ona da bir bakalım.

Her bir noktanın ortalamaya uzaklığının karesine de Ortalamaya Uzaklığın Kareler Toplamı (OUKT) diyelim.
Ortalamaya Uzaklığın Kareler Toplamı (OUKT) = TOPLAM(y_i – ȳ)²

R² ise bu iki değerden faydalanılarak hesaplanır.

R2 = 1 - (AKT/OUKT)

Artıkların toplamının ortalamaların toplamına olan oranı ne kadar küçük ise R² o kadar yüksek olacaktır.

R²‘ın yüksek olması regresyon model uyumunun iyi olduğunu gösterir. Yukarıda da söylediğimiz gibi tüm noktalar regresyon doğrusu üzerinde olsaydı mükemmel bir modelimiz olurdu. Tüm noktalar doğru üzerinde olduğunda Artıkların Kareler Toplamı (AKT) sıfır olacağından R²‘e de 1’e eşit olacak ve alabileceği en yüksek değeri alacaktır.

Peki ya düzeltilmiş R Kare ?

Yukarıda basit regresyon (tek bağımsız değişkenli) üzerinden örnek verdik. Ancak gerçek hayatta bağımlı değişkeni etkileyen birden fazla bağımlı değişken vardır. Regresyon iyilik uyum indeksi (goodness of fit) olarak R² kullandığımızda artıkların toplam karesi ne kadar düşük olursa uyum o kadar yüksek oluyor. Ancak bağımsız değişken sayısı arttıkça payda düşmeye devam edecektir. Böylelikle  R² düşmeyecek ve ne kadar çok değişken modele katılırsa o kadar yüksek bir uyum ortaya çıkacaktır. Acaba gerçekte de öyle mi? Model karmaşıklığını azaltmak ve anlaşılabilir, yorumlanabilir (interpretable) modeller oluşturmak için hedef değişkene etkisi olmayan, az olan, etkisi ihmal edilebilen değişkenler modele dahil edilmez ve kafalar bulandırılmaz. Bu sebeple iyilik uyum indeksi kullanırken R² geliştirerek düzeltilmiş R² kullanılmaktadır. Düzeltilmiş R² ‘nin R² ‘den farkı gereksiz eklenen bağımsız değişkenleri cezalandırıyor olmasıdır. Formülde bunun nasıl olduğunu görelim:

p: bağımsız değişken sayısı, n: örneklem büyüklüğü

Aslında formüldeki 1 – R² , artıklar kareler toplamının ortalamaya uzaklıklar kareler toplamına oranıdır (AKT/OUKT). Bu oran zaten R² ‘nin temelini oluşturuyordu. Bu oran, başka bir oran ile çarpılarak düzeltilmiş sadece. O da örneklem büyüklüğü ve bağımsız değişken sayısının da içinde bulunduğu oran: (n-1)/(n-p-1). Formülde yeni orana dikkat edecek olursak n-1’in n-1’e bölümü 1’dir yani bir şeyi değiştirmez. Ancak paydada n’den değişken sayısı olan p çıkarılarak bu oranın 1’den büyük olması sağlanıyor. Oran 1’den fazla olacağı için Düzeltilmiş  R² ‘yi azaltacaktır. İşte gereksiz değişkenler yüzünden model uyumunun cezalandırılması yoluyla elde edilen yeni uyum indeksi, düzeltilmiş  R² ‘dir ve  R² ‘den daha sağlıklı bir metrik, uyum indeksi oluşturur.

İyi kareler…