R ile Zaman Serileri Çözümlemesi Bölüm 3 (Ayrıştırma Yöntemleri)

Osman IŞIK 16 Nisan 2019 Genel bir bakış 2 4334 1704 kelime - 11 dakika93

---

Bu yazıya puan ver

(No Ratings Yet)

Loading...

---

Merhaba Veri Bilimi Okulu sevenler bu yazımızda zaman serisi modellerinden olan Ayrıştırma Yöntemlerinden bahsedeceğiz. Bir zaman serisi trent(T_t), mevsimsel dalgalanma(M_t), döngüsel hareket (C_t) ve düzensiz rasgele hareketlere sahip hata bileşenlerinden (ε_t) oluşmaktadır. Bu bileşenleri ayırarak her bir bileşen için tahminleri içeren ve bu bileşenlerin tahmininden zaman serisinin öngörüsünü hesaplayan yönteme ayrıştırma yöntemleri denir. Matematiksel olarak,  Z_t=f(T_t, M_t , C_t, ε_t) şeklinde gösterilip tahmini ise : Z =f(T_t, M_t , C_t)’dir. Bilinen en eski öngörü yöntemlerinden olup kısa dönemli öngörülerde anlaşılması ve yapılması en kolay yöntemdir. Trende ve Mevsimselliğe sahip verilerde kullanılır.  Ayrıştırma Yöntemleri Toplamsal ve Çarpımsal olmak üzere 2 yöntemdir.

Toplamsal Ayrıştırma Yöntemi:

Trent, mevsimsellik ve hata bileşenlerinin toplanmasıyla oluşup şu şekilde formüle sahip modeldir:

Z_t = T_t + M_t + ε_t

Burada hata teriminin(ε_t) rasgele bir harekete sahip olması gerektiğine dikkat edilmelidir.

Çarpımsal Ayrıştırma Yöntemi:

Trent, mevsimsellik bileşenlerinin çarpılması ve hata bileşeninin toplanmasıyla oluşup şu şekilde formüle sahip modeldir:

Z_t = T_t * M_t + ε_t

Bu yöntemin uygulanışı bazı noktalarda toplamsal ayrıştırma yönteminden farklılık gösterir ama temel mantık olarak bu iki model arasında pek bir farklılık yoktur.

Modellerin Sağlaması Gereken Varsayım:

i-) Ayrıştırma yönteminin hata bileşeni akgürültü serisi olması yani hataların arasında ilişki olmaması.

Şimdi gerekli bilgiler verildikten sonra R ile uygulamaya geçebiliriz.

R ile TOPLAMSAL AYRIŞTIRMA ÇÖZÜMLEMESİ

Adım 1-) Veri seti ve hazırlanması ve Zaman Serisi Grafiği:

#Gerekli paketin yüklenmesi ve çağırılması
install.packages("fpp")
library(fpp)
#yüklenen paketteki veri seti
veri<-data(ausbeer)
#Veri setinin azaltılması
zs_bira = tail(head(ausbeer, 17*4+2),17*4-4)
#Zaman Serisi Grafiği
plot.ts(zs_bira)

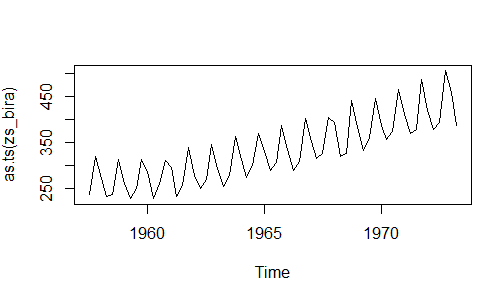
Zaman Serisi Grafiğine baktığımızda artan bir trende ve mevsimselliğe sahip olduğunu görüyoruz bu tip grafiklere sahip seriler genellikle Toplamsal Ayrıştırma Modeline uygun serilerdir.

Adım 2-) Merkezsel Hareketli Ortalama (MHO) Serisi:

Trent eğilimini belirlemek için seriyi “merkezsel hareketli ortalama” metodunu kullanırız. Ayrıştırmayı yapmak için periyodu bilmemiz şart o yüzden burada koymadım ama bir önceki yazıdaki gibi periyodu tespit  edebiliriz, bu seri için periyodumuz 4’tür.

install.packages("forecast")
library(forecast)
trent_bira = ma(zs_bira, order = 4, centre = T)
plot.ts(zs_bira)
lines(trent_bira)
plot.ts(trent_bira)

Grafikler:

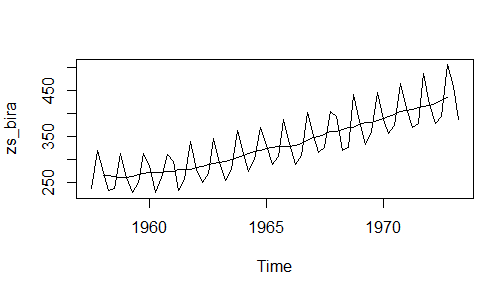
Zaman serisi grafiği ve ortadaki çizgi ise trent bileşenini gösteriyor.

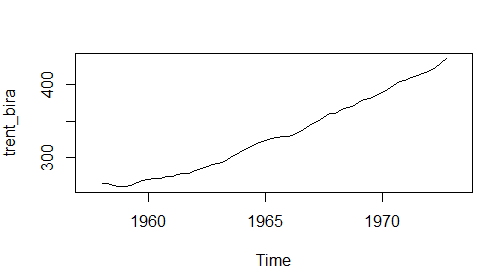
Yukarıdaki grafik ise trend bileşenin grafiğini göstermektedir, bakıldığında artan bir trendin olduğu apaçık bellidir.

Adım 3 -) Orijinal Seriden MHO serisini çıkartmak:

Mevsimsel bileşene ulaşmak için yukarıda hesapladığımız merkezsel hareketli ortalama serisini, orijinal seriden çıkartmamız gereklidir.

#Orj-MHO
detrent_bira = zs_bira - trent_bira
plot.ts(detrent_bira)

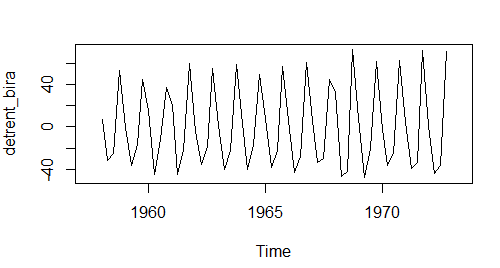
Yukarıdaki grafiğe baktığımızda orijinal seriden trend bileşeninin ayrılmış halini görürüz ama bu seride mevsimsel bileşen ile hata bileşeni vardır bu yüzden aşağıdaki adımı uygulayıp mevsimsel bileşeni buluruz.

Adım 4-) Periyottaki Dönemlerin Ortalama Değerlerinin Hesaplanması:

Elde edilen periyottaki dönemlerin ortalama değerlerinin toplamı 0 olmalıdır. Eğer bu toplam 0 değilse ortalama değerlerinin ortalaması alınır ve bu ortalama değer diğer ortalama değerlerden çıkartılır bu sayede 0 olmuş olur. Bu yaptığımız işlem sonucunda mevsimsel bileşeni buluruz. Bu seri orijinal serinin saf mevsimsel bileşenidir.

m_bira = t(matrix(data = detrent_bira, nrow = 4))
mevsimsel_bira = colMeans(m_bira, na.rm = T)
plot.ts(rep(mevsimsel_bira,16))

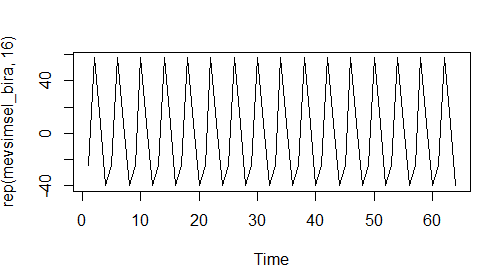
Yukarıdaki grafikte mevsimsel bileşeni görüyoruz. Şimdi ise geriye bir tek hata bileşeni bulmak kalıyor bunun için aşağıdaki adım yapılır.

Adım 5-) Hata Bileşenin Hesaplanması:

Hata bileşenini orijinal seriden trend ve mevsimsel bileşenlerini çıkartarak buluruz.

hata_bira = zs_bira - trent_bira - mevsimsel_bira
plot.ts(hata_bira)

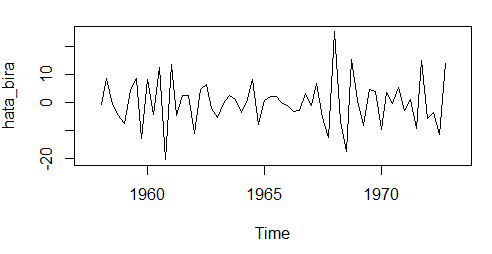
Yukarıdaki grafikte hata bileşenini görüyoruz. Şimdi bileşenleri teker teker toplayarak orijinal seriyi elde edebiliyor muyuz ona bakalım.

Adım 6-) Orijinal Serinin Tekrardan Elde Edilmesi ve Tahmin Serisinin Hesaplanması:

orj_seri = trent_bira + mevsimsel_bira + hata_bira
plot.ts(orj_seri)
#Tahmin Serisi = Trent Bileşeni + Mevsimsel Bileşen
tahmin_serisi = trent_bira + mevsimsel_bira
plot.ts(tahmin_serisi)

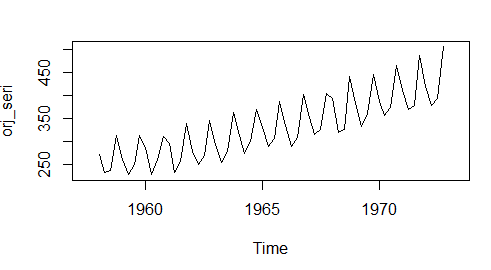
Orijinal Serinin Zaman Serisi Grafiği

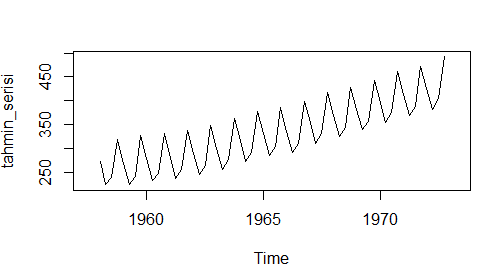
Tahmin Serisinin Zaman Serisi Grafiği

Evet yukarıdaki zaman serisi grafiğine baktığımızda aynı seriyi elde etmiş olduk ve ayrıca tahmin serisine baktığımızda da orijinal seri ile aynı gibi duruyor neyse bu konuya birazdan değineceğiz 🙂 . Sağlaması gereken koşullara bakmadan önce sizden bir isteğim var bu yukarıda yapmış olduğum işlemlerin daha kolay yapılışı var. Bunu en başta göstermediğim için lütfen bana kızmayın amacım ayrıştırma yöntemlerinin temel mantığını zihninizde oturtmaktı o yüzden hemen yukarıda yaptığımız işlemlerin kısa yolunu gösterip daha sonra gerekli varsayımlara bakalım. Hatta Çarpımsal Ayrıştırmayı’da kısa yoldan yapalım, zaten mantık aynı sadece orada toplamalar çarpma, çıkarmalar bölme oluyor (hata bileşeni hariç). Hadi kısa yoldan yapalım.

Ayrıştırma yöntemlerini kısa yoldan yapmak için  DECOMPOSE() fonksiyonu kullanılıyor daha kolay ve daha kullanışlıdır, neyse lafı daha fazla uzatmadan buyurun yapalım.

DECOMPOSE() Fonksiyonu:

install.packages("stats")
library(stats)
zs_bira <- ts(zs_bira, frequency = 4)
decompose_bira <- decompose(zs_bira, "additive")
plot.ts(decompose_bira$seasonal) #mevsimsel bileşen
plot.ts(decompose_bira$trend) #trent bileşeni
plot.ts(decompose_bira$random) #hata bileşeni
plot(decompose_bira)# Orijinal seri, trent, mevsimsel ve hata serisinin tamamını gösterir.

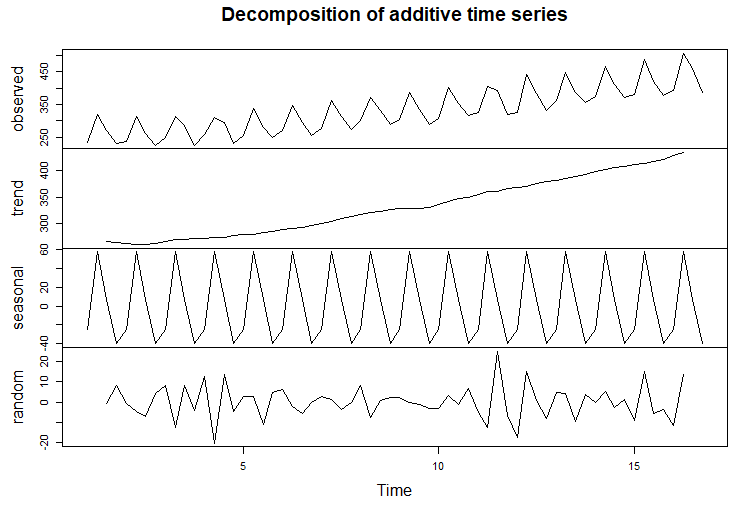
Yukarıdaki grafikte orijinal seri, trent, zaman ve hata bileşenlerini görüyoruz. Şimdi sağlaması gereken varsayıma bakalım.

1. Varsayım hatalar arasında bir ilişki olup olmaması:

İlişkileri test etmeden önce ilk işimiz aşağıdaki gibi hipotez kurmaktır.

Ho: Hatalar arasında ilişki vardır.

Hs: Hatalar arasında ilişki yoktur.

Hipotezimizi kurduktan sonra Box Ljung test istatistiği ile bu hipotezi test ederiz. Hipotezin reddedilmesini isteriz ki bu model ile öngörü yapmak isteyelim. Aşağıdaki kodda yazıldığı gibi kolay bir test ile bu varsayıma bakabiliriz. Ayrıca diğer bir kod ile de grafiklerine bakarak yorumlayabiliriz.

library(stats)
Box.test(decompose_bira$random)
library(forecast)
checkresiduals(decompose_bira$random, lag = 24)

Çıktılar:

Yukarıdaki çıktıya baktığımızda yokluk hipotezimizin (H0) reddedildiğini görüyoruz p-değeri < α =0.05’den küçük olduğu için. Yani hataların arasında ilişki olmadığını söyleyebiliriz. Hatalar arasında ilişki olmaması demek ne demek peki? Hataların arasında ilişki olamaması hataların normal dağılıma yakınsadığını gösterir. Bunu açıklamamın sebebi aşağıdaki grafikleri yorumlarken göreceğiz.

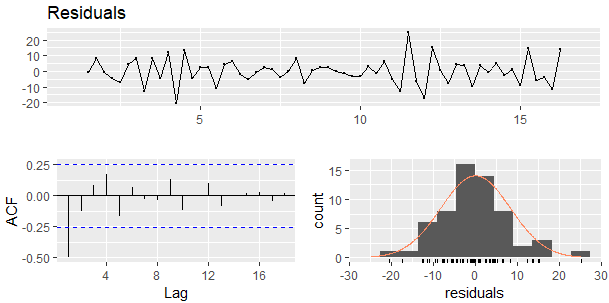
Evet yukarıdaki grafiklere baktığımızda ilk grafiği ilk başta yaparken gördüğümüz hata bileşenine ait olduğunu görüyoruz ve altındakiler ise ACF ve Hataların histogram grafiği. Histogram grafiğine baktığımızda hafif sağa çarpık bir dağılım olduğunu ama normal dağılıma da uyduğunu görüyoruz. Toplamsal ayrıştırma yöntemi de bittiğine göre sıradaki yöntemimize geçebiliriz.

R ile ÇARPIMSAL AYRIŞTIRMA ÇÖZÜMLEMESİ

Yukarıda söylediğim gibi bunu kısa yoldan hemen yapacağız.

#ÇARPIMSAL AYRIŞTIRMA YÖNTEMİ
#Veri setinin hazırlanması
install.packages("Ecdat")
library(Ecdat)
data("AirPassengers")
zs_hava <- AirPassengers
plot.ts(zs_hava)

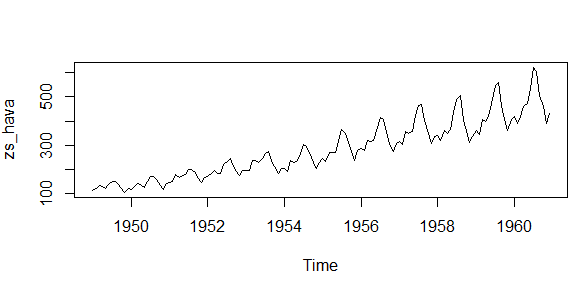
Yukarıdaki grafiğe baktığımızda artan bir trende ve artan bir mevsimsel dalgalara saihp olduğunu görüyoruz. Bu tür grafiğe sahip verilerde genellikle Çarpımsal Ayrıştırma Yöntemi kullanılır.

Bu yöntemi yaparken de periyodumuzun 12 olduğunu ama periyodu önceki yazıda nasıl bulduğumuzu gösterdiğim için burada da yapmayacağım direkt olarak yapıp geçeceğim.

install.packages("stats")
library(stats)
zs_hava <- ts(zs_hava, frequency = 12)
decompose_hava <- decompose(zs_hava, "multiplicative")
plot.ts(decompose_hava$seasonal) #mevsimsel bileşen
plot.ts(decompose_hava$trend) #trent bileşeni
plot.ts(decompose_hava$random) #hata bileşeni
plot(decompose_hava)# Orijinal seri, trent, mevsimsel ve hata serisinin tamamını gösterir.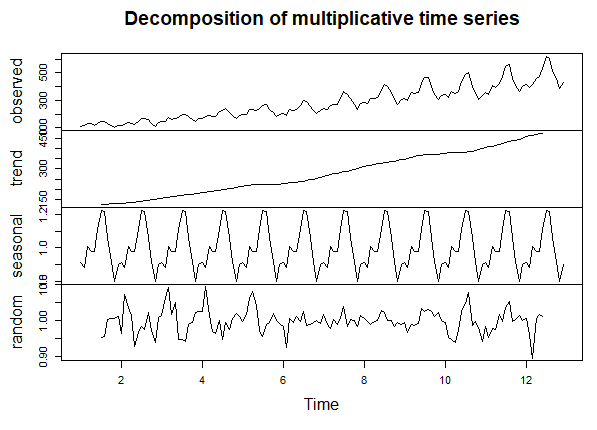

Yukarıdaki grafikte orijinal seri, trent, zaman ve hata bileşenlerini görüyoruz. Şimdi sağlaması gereken varsayıma bakalım.

1. Varsayım hatalar arasında bir ilişki olup olmaması:

İlişkileri test etmeden önce ilk işimiz aşağıdaki gibi hipotez kurmaktır.

Ho: Hatalar arasında ilişki vardır.

Hs: Hatalar arasında ilişki yoktur.

Hipotezimizi kurduktan sonra bunu da Box Ljung test istatistiği ile test ederiz. Aşağıdaki kod ile hemen test edelim.

library(stats)
Box.test(decompose_hava$random)

Çıktı:

Yukarıdaki çıktıya baktığımızda yokluk hipotezinin(H0) reddedildiğini görüyoruz. Yani hatalarımızın arasında ilişki olmadığını yani akgürültü olduğunu söyleyebiliriz.

Bu yöntemde bittiğine göre diğer yöntemlerde görüşmek üzere 🙂 Sağlıcakla kalınız…

Çözümlemede Kullanılan Kaynaklar:

https://anomaly.io/seasonal-trend-decomposition-in-r/

Cem Kadılar-SPSS Uygulamalı Zaman Serileri Analizine Giriş

Dipnot: Kullandığım kodlar ve veri setleri yukarıda kaynaklarda verdiğim internet sitesinden alıntılanmış olup anlatım, kurulan hipotezler ve yorumlar bana aittir.