R ile Zaman Serileri Çözümlemesi Bölüm 1

Osman IŞIK 21 Aralık 2018 Uygulama 0 4676 654 kelime - 4 dakika87

---

Bu yazıya puan ver

(2 votes, average: 3,00 out of 5)

Loading...

---

Zaman kavramı yüzyıllardır her insan için merak kaynağı olmuştur. İnsanlar geleceğe yönelik tahmin veya öngörü yapmak istemişlerdir ve bu durum sadece insanlar için değil bilim dalları içinde ilham kaynağı olmuştur. Hatta Einstein, Stephen Hawking gibi bilim insanları da bu kavram için çalışmıştır.Tabi her bilimde olmazsa olmaz illa kendine bir yer edinen İstatistik bilimi de zamanla ilgili çalışmak istemiştir.Biz de Veri Bilimi Okulu ailesi olarak bu noktada Zaman Serileri Çözümlemelerini R ile sizlere takdim ediyoruz. O zaman daha fazla lafı uzatmadan başlayalım.

Zaman Serisi Grafikleri:

Sadece Zaman Serisi’nde değil herhangi bir veri çözümlemesinde de çözümlemeye başlamadan önce yapılacak ilk şey veri görselleştirmektir. Veri görselleştirme bize veriler hakkında ne yapacağımızı gösterir.  Zaman serisi grafikleri de verinin çözümlemesinde ne yapacağımıza ipuçları verir.

Hemen bir zaman serisi oluşturalım ve  bunu daha sonra görselleştirelim.

ts komuduyla serimizi oluşturalım ve grafiğini çizdirelim.

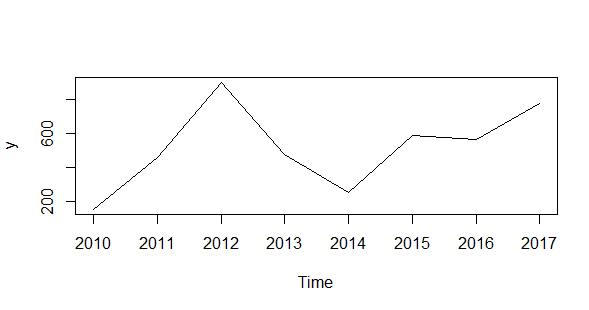
y <- ts(c(158,458,895,475,255,587,562,775), start =2010 )
plot.ts(y) #Basit görselleştirme

Çıktı:

Şimdi ise R’daki fpp2 kütüphanesindeki verisetlerinden sunspot.year isimli senelik veriler üzerinden ggplot2 kütüphanesi yardımıyla görselleştirelim.

autoplot(sunspot.year) +
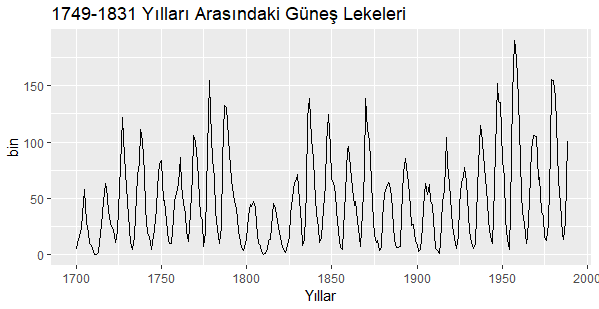
  ggtitle("1749-1831 Yılları Arasındaki Güneş Lekeleri") +
  xlab("Yıllar") +  ylab("bin")

Çıktı:

Zaman Serisi Bileşenleri:

Trent: Bir serinin belli bir zaman boyunca artması veya azalması hareketine denir.

Mevsimsellik: Seride senelik,aylık,haftalık gibi faktörlerden etkilenerek oluşan kavramdır.

Otokorelasyon Fonksiyonu:

Korelasyon, iki değişken arasındaki doğrusal ilişkinin ölçüsünü ölçerken, otokorelasyon bir zaman dizisinin gecikmeli değerleri arasındaki doğrusal ilişkiyi ölçer .Örneğin r1, yt ile yt-1 arasındaki ilişkiyi ölçer. r2, yt-1, yt-2 arasındaki ilişkiyi gösterir ve fonksiyon,

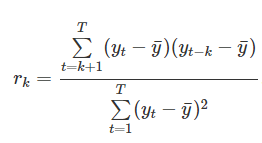
Otokorelasyon yani ACF Grafiği:

ggAcf(beer, lag.max = 56)

Çıktı:

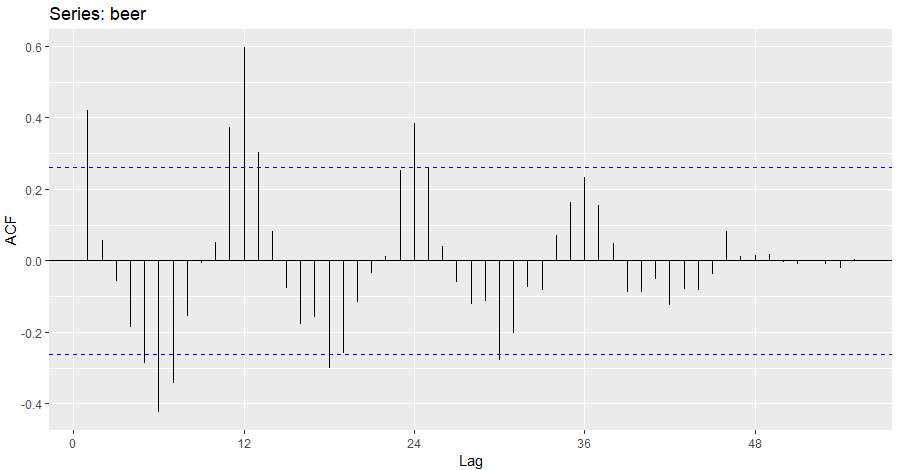
Gecikme sayısı 56 olan ACF grafiği. Mavi çizgiler güven sınırlarını gösterir.Yukarıdaki ACF grafiğine baktığımızda Trende sahip bir verinin ACF grafiğini görmekteyiz. İlk 4 gecikme güven sınırları dışındaysa trendin olduğunu söyleyebiliriz. Şimdi mevsimselliğe ve trende sahip bir serinin Zaman Serisi Grafiğine ve ACF grafiğine bakalım.

aelec <- window(elec, start=1980)
autoplot(aelec) + xlab("Year") + ylab("GWh")
ggAcf(aelec,,lag.max = 56)

Grafikler:

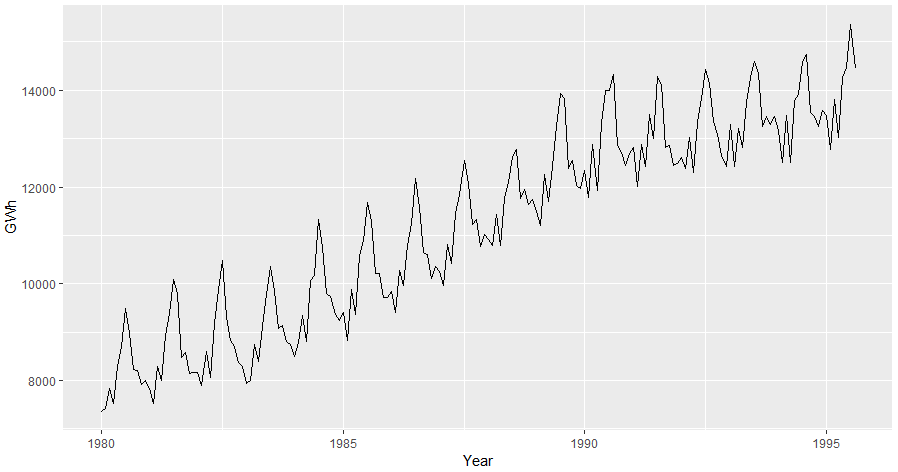
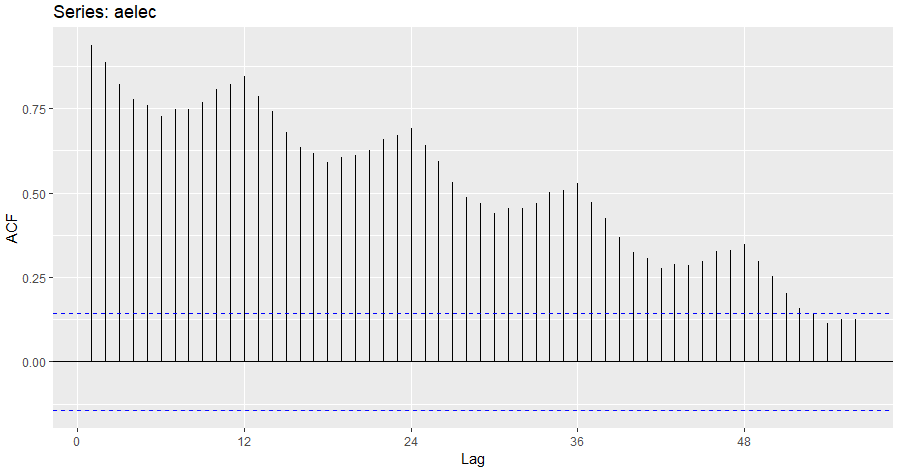
Zaman serisi ve ACF Grafiklerine baktığımızda bu grafiklerin trende ve mevsimselliğe sahip olduğunu söyleyebiliriz.

Kısmi Otokorelasyon Fonksiyonu:

Zaman serileri analizinde, kısmi otokorelasyon fonksiyonu (PACF), bir zaman dizisinin kendi gecikmeli değerleri ile kısmi korelasyonunu verir ve tüm kısa süreli gecikmelerde zaman serilerinin değerlerini kontrol eder ve fonksiyon,

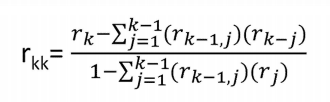
Trende sahip kısmi otokorelasyon yani PACF Grafiği:

ggPacf(beer, lag.max = 42)

Çıktı:

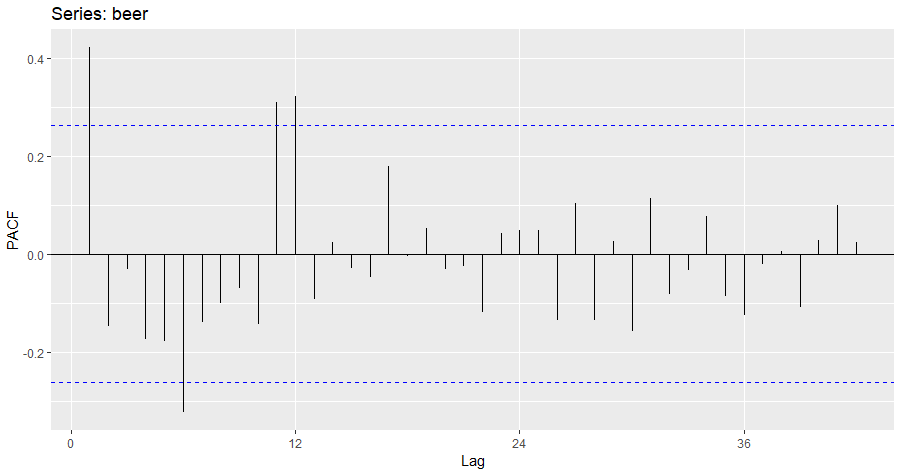
Trende sahip 42 gecikmeli kısmi otokorelasyon grafiği(PACF)

Mevsimselliğe ve Trende Sahip PACF Grafiği:

aelec <- window(elec, start=1980)
ggPacf(aelec,lag.max = 42)

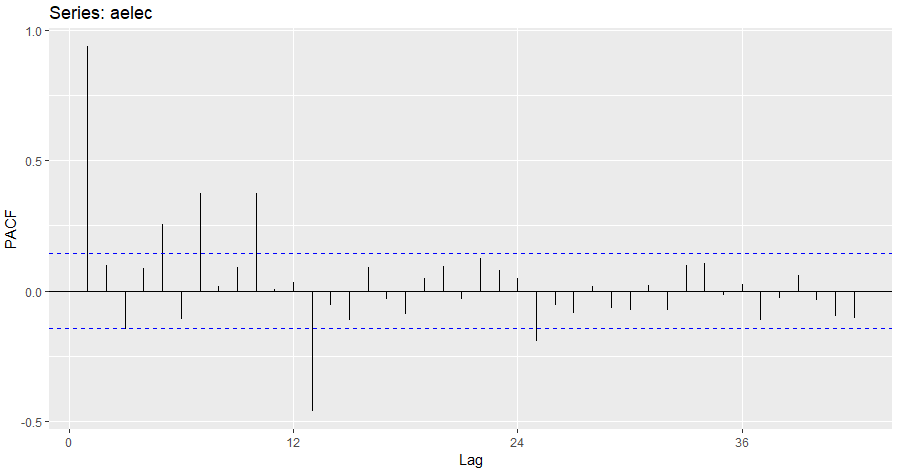
Trende ve mevsimselliğe sahip 42 gecikmeli PACF grafiği

Akgürültülük:

Eğer bir seri hiçbir ilişkiye sahip değilse bu seriye akgürültü serisi denir.

set.seed(30)
y <- ts(rnorm(50))
autoplot(y) + ggtitle("Akgürültü")
ggAcf(y)

Çıktılar:

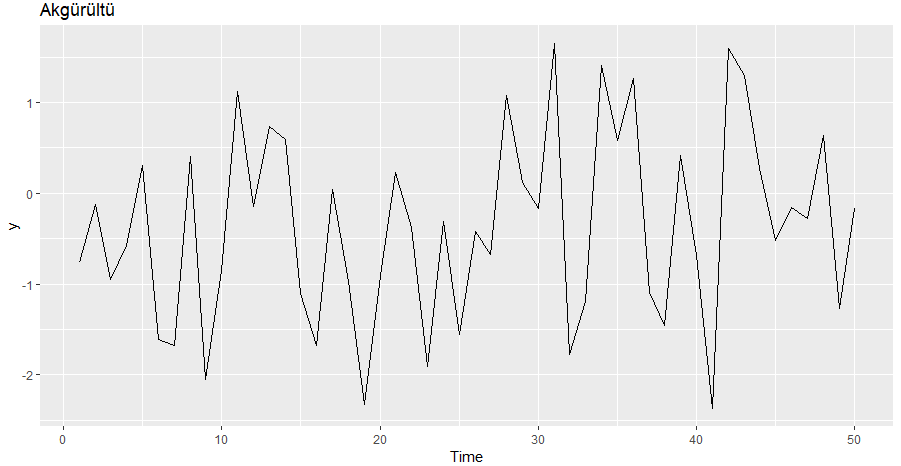
Akgürültü Serisinin Zaman Serisi Grafiği

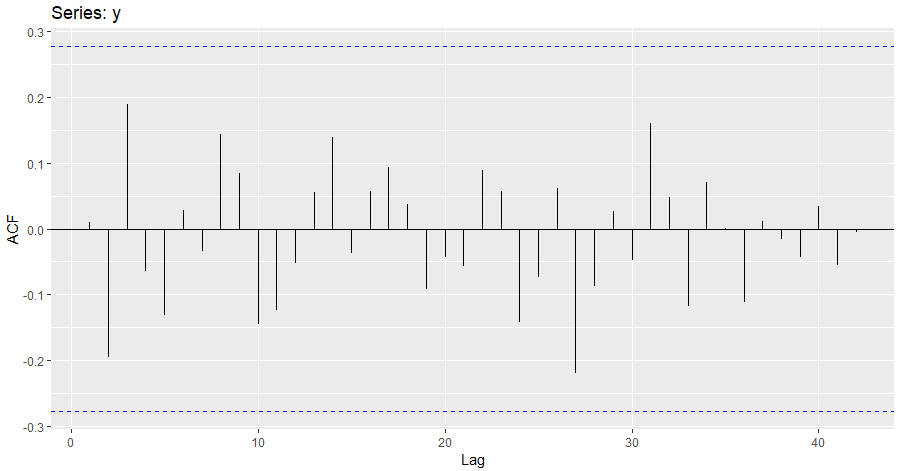
42 gecikmeye sahip akgürültü serisinin ACF Grafiği

Akgürültü serisinin ACF grafiğindeki bütün gecikmeler güven sınırlarının altında olur.

Zaman serilerinde gerekli olan temel kavramları verdikten sonra bir sonraki yazımızda görüşmek üzere 🙂

Saygılarımla…

Çözümlemede Kullanılan Kaynaklar:

https://otexts.org/fpp2/wn.html

https://stackoverflow.com/questions/44641981/how-to-extract-a-table-of-the-acf-values

Cem Kadılar-SPSS Uygulamalı Zaman Serileri Analizine Giriş