
![]()
Merhaba Veri Bilimi Okulu severler uzun bir aradan sonra tekrardan sizlerleyim. Zorlu geçen final haftasından sonra kafamı topladıktan sonra serinin geri kalan yazılarını tamamlamak için tekrardan buradayım. Daha fazla lafı uzatmadan ne yapacağımızı açıklayayım, zaman serisi analizi yapmadan önce temel işlemleri R programlama ile göstereceğim. Bir önceki yazımızda da gerekli temel kavramları göstermiştim o yazıya da buradan ulaşabilirsiniz. Zaman serisi, ACF, PACF grafikleri çizdirmek, otokorelasyon(ACF) ve kısmi otokorelayon(PACF) tabloları çıkarmak ve fark alma işlemlerinden bahsedeceğim.
Öncelikle seriyi çözümlemeye başlamadan evvel ilk işimiz seri hakkında bilgi almak için zaman serisi grafiği çizdirmektir. Aşağıda zaman serisi grafiği çizdirmek için gerekli olan kodları ve çıktılarını görebilirsiniz.
ZAMAN SERİSİ GRAFİKLERİ:
#Gerekli Kütüphaneler library(fpp2) library(fpp2) #Öngörü için uygulama verileri içeren kütüphane library(ggplot2) library(ggplot2) #Veri görselleştirilmesi yapmak için kullanılan kütüphane y <- ts(c(158,458,895,475,255,587,562,775), start =2010 ) plot.ts(y)
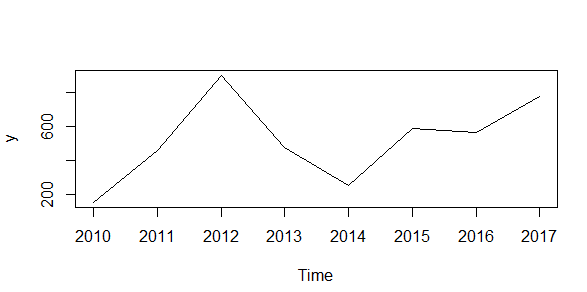
autoplot(sunspot.year)
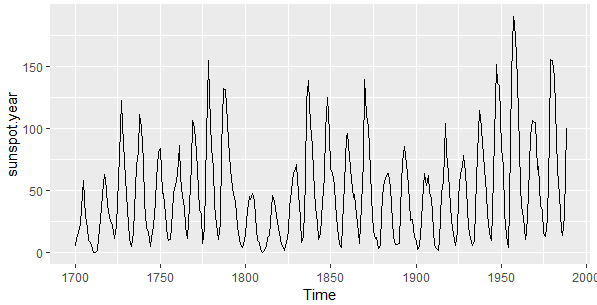
ACF GRAFİKLERİ:
ggAcf(y)
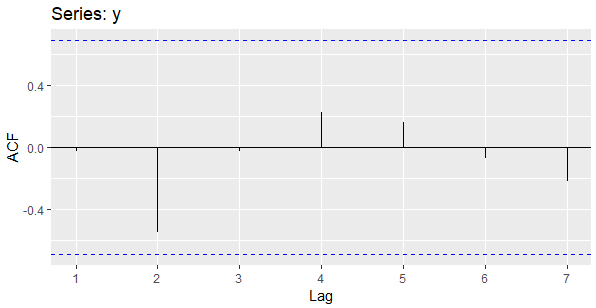
ggAcf(sunspot.year)
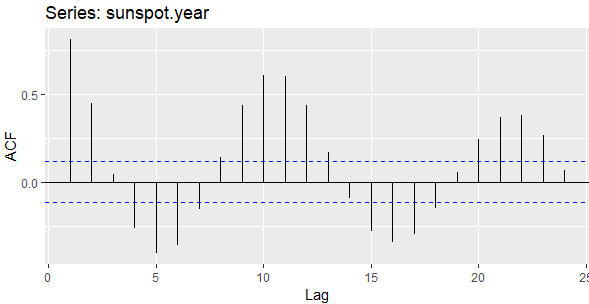
PACF GRAFİKLERİ:
ggPacf(y)
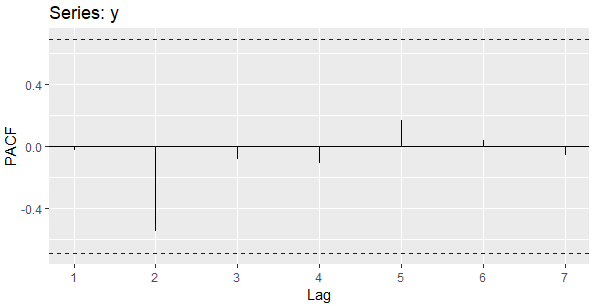
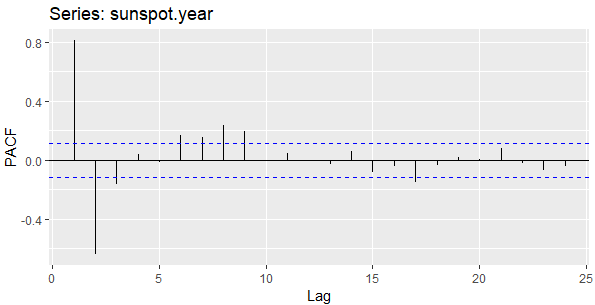
ggPacf(sunspot.year)
OTOKORELASYON(ACF) TABLOSU
y_acf <- acf(y,plot=F)

sunspot_acf <- acf(sunspot.year, plot = F)
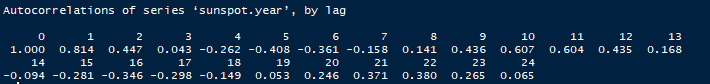
KISMİ OTOKORELASYON(PACF) TABLOSU
y_pacf <- pacf(y, plot = F)

sunspot_pacf <- pacf(sunspot.year, plot = F)
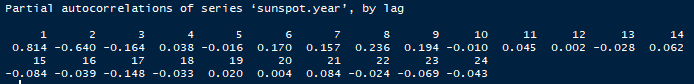
FARK ALMA İŞLEMLERİ
Fark alma işlemleri seriyi trent ve mevsimsellikten arındırıp seriyi durağan hale getirmek için yapılır. Trent için yapılan farka i. dereceden fark(i kaç kere fark alınmışsa onu gösterir), mevsimsellikten arındırmak için yapılan farka i.dereceden mevsimsel fark(i kaç kere mevsimsel fark alınmışsa onu gösterir) denir. R’da her iki fark içinde “forecast” kütüphanesindeki diff() fonksiyonu kullanılır. Aşağıdaki örneklerle daha rahat anlaşılacağını düşünüyorum o yüzden buyurun örneklere beraber bakalım.
#Veri Setinin yüklenmesi
library(haven)
I0 <- read_sav("C:/Users/asus/Desktop/DERSLER/İST477-ZAMAN DİZİLERİ ÇÖZÜMLEMESİ/1. hafta/I0.sav")
head(I0)
#Zaman Serisi Grafiği Çizimi ve yorumlanması plot.ts(I0)
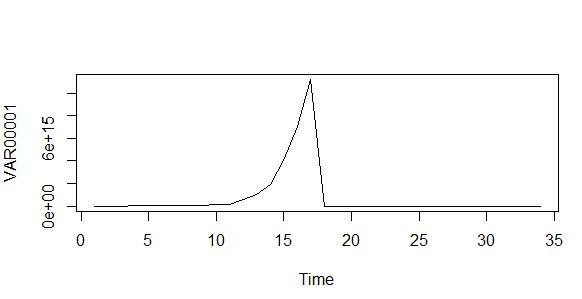
Yukarıdaki zaman serisi grafiğine bakıldığında 10. zamanda ani bir sıçrama olduğu görülüyor bu bize serinin trende sahip olabileceği düşüncesine götürüyor ama kesin sonuç için her zaman ACF ve PACF grafiklerini çizdirmekte fayda vardır.
#ACF ve PACF Grafikleri I0_acf <- acf(I0, plot = T, lag.max = 42) #42 gecikmeye sahip ACF Grafiği I0_acf #ACF Tablosu I0_pacf <- pacf(I0, plot = T, lag.max = 42) #42 gecikmeye sahip PACF Grafiği I0_pacf #PACF Tablosu
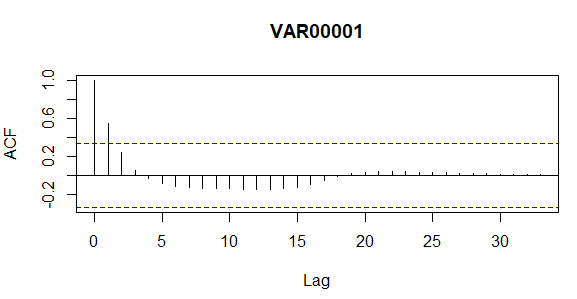

Serinin trende sahip olduğunu anlamamız için ACF Grafiğindeki ilk 4 gecikmenin aynı anda sınırlar dışarısında kalması gerekir, yukarıdaki grafiğe baktığımızda serinin trende sahip olmadığını görüyoruz bu seri durağandır ve bu seriye herhangi bir fark işlemi uygulamadan direkt olarak çözümlemelere başlayabiliriz. PACF grafik ve tablosuna da bakalım.
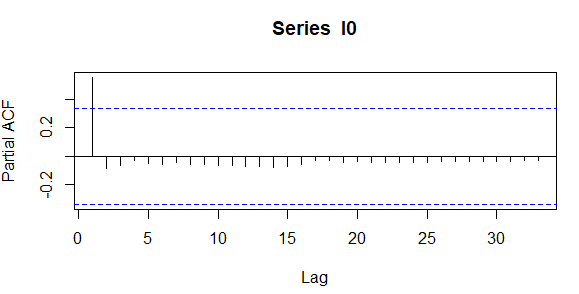

Şimdi bir başka bir veri setini inceleyelim.
#Veri Setinin yüklenmesi
I1 <- read_sav("C:/Users/asus/Desktop/DERSLER/İST477-ZAMAN DİZİLERİ ÇÖZÜMLEMESİ/1. hafta/I1.sav")
head(I1)
#Zaman Serisi Grafiği Çizimi ve yorumlanması plot.ts(I1)
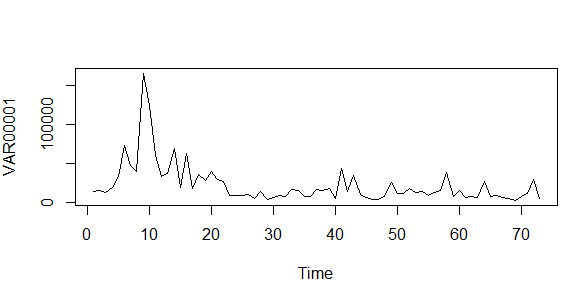
Yukarıdaki zaman serisi grafiğine bakıldığında, seride zaman zaman sıçramalar ve dalgalanmalara sahip olduğu görülüyor bu bize serinin trende ve mevsimselliğe sahip olabileceğinden şüphelendiriyor bunu anlamak için ACF ve PACF grafiklerine bakalım.
#ACF ve PACF grafikleri acf(I1, plot = T, lag.max = 42) pacf(I1, plot = T, lag.max = 42)
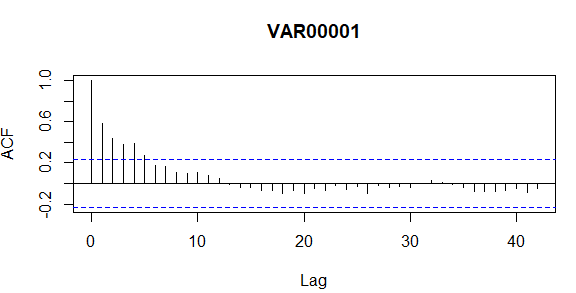
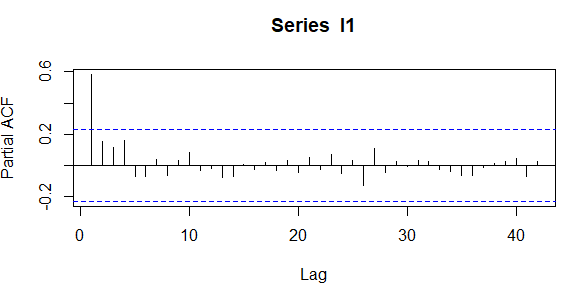
ACF Grafiğine bakıldığında ilk 4 gecikme ve hatta 6 gecikmenin sınırlar dışarısında olduğunu görüyoruz bu serinin kesin trende sahip olduğunu söyleyebiliriz trendden kurtulmak için 1. dereceden fark almamız gerekir.
#Birinci Dereceden Mevsimsel Olmayan Fark Alma I1_birinci_d_fark <- diff(I1$VAR00001, differences = 1) acf(I1_birinci_d_fark,lag.max = 42) pacf(I1_birinci_d_fark, lag.max = 42)
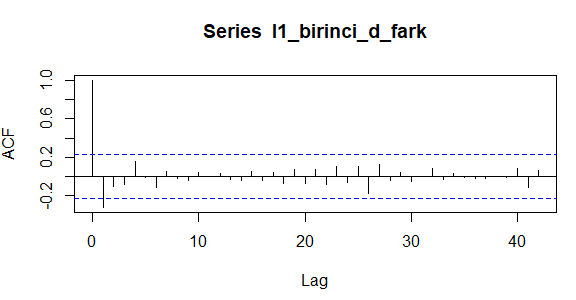
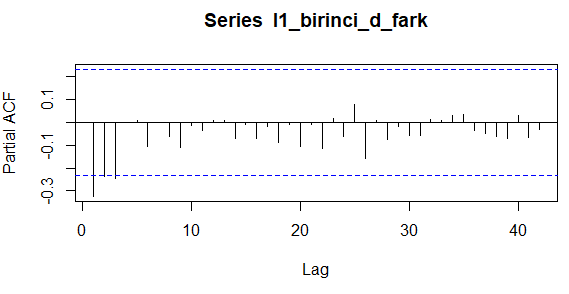
Yukarıdaki ACF grafiğine bakıldığında serinin trendden kurtulduğunu görüyoruz. Bu seri sadece trende sahip bir seri olmakla beraber sadece 1 kere mevsimsel olmayan fark almamız seriyi durağanlaştırmak için yetti.
Şimdi ise sadece mevsimselliğe sahip bir veri setinde fark alma işlemi yapalım.
#Veri yükleme
veri <- read_sav("C:/Users/asus/Desktop/DERSLER/İST477-ZAMAN DİZİLERİ ÇÖZÜMLEMESİ/1. hafta/I016.sav")
head(veri)
#Zaman Serisi Grafiği plot.ts(veri)
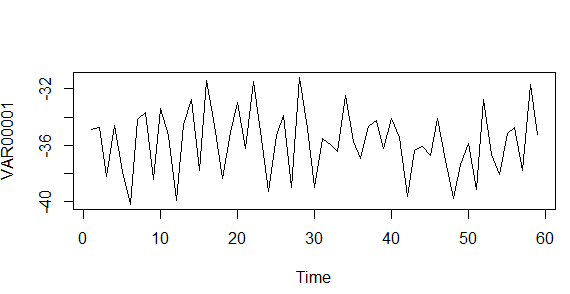
Yukarıdaki zaman serisi grafiğine bakıldığında dalgalanmaların çok olduğu görülüyor bu bizi mevsimsellikten şüphelendiriyor ama kesin sonuç için ACF ve PACF grafiklerine bakmamız lazım.
#ACF, PACF Grafikleri ve Tabloları acf(veri, lag.max = 42) veri_acf_tablosu <- acf(veri, lag.max = 42, plot = F) #Periyot 6 veri_acf_tablosu pacf(veri, lag.max = 42) veri_pacf_tablosu <- pacf(veri, lag.max = 42, plot = F) veri_pacf_tablosu
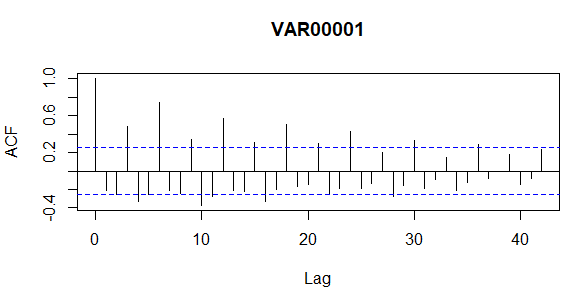
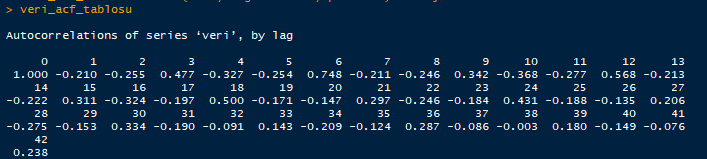
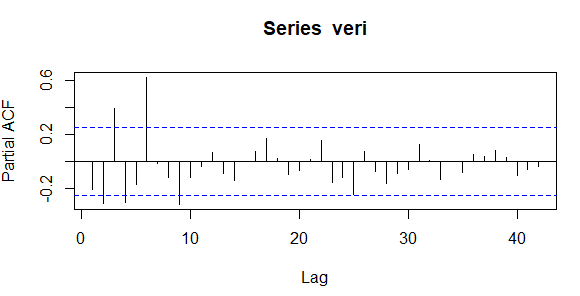

Yukarıdaki ACF grafiğinden seride mevsimellik olduğu görülüyor, gecikmelerdeki dalgalanmalardan ötürü mevsimsel fark almamız şart ama mevsimsel fark almadan önce periyodu belirlememiz lazım o yüzden ACF ve PACF grafik ve tablolarına bakmamız lazım.
Periyodu belirlemek için ACF grafiğindeki pozitif taraftaki en büyük 1. gecikme ile en büyük 2. gecikmeyi bulmamız lazım eğer grafikten fark edemiyorsak tablodan yardım alabiliriz ama burada gerek yok çünkü ACF grafiğinde gecikmelerin büyüklüğü net bir şekilde ayırt edilebiliyor. Aşağıdaki görseldeki gibi periyodu belirliyoruz.
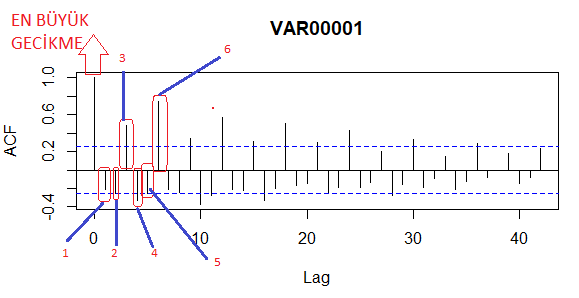
En büyük gecikme değil bir sonraki gecikmeden saymaya başlayarak en büyük 2. gecikmeye kadar saymaya başlıyoruz. Buradaki en büyük 2 .gecikme 6 ile numaralandırılmış gecikmedir. Ayrıca PACF Grafiğine bakıldığında 6. gecikmenin göze batar bir şekilde sınırlar dışarısında kaldığı görülüyor buradan da periyodun 6 olduğuna emin olabiliyoruz. Yani bu seride periyot 6 olarak çıkmıştır. Periyot belirlendiğine göre mevsimsel fark alabiliriz.
#Mevsimsel fark alma veri_birinci_mev <- diff(veri$VAR00001,6) acf(veri_birinci_mev, lag.max = 42) pacf(veri_birinci_mev, lag.max = 42)
Mevsimsel fark aldıktan sonra mevsimselliğin bitip bitmediğini görmek için ACF ve PACF grafiklerine bakılır.
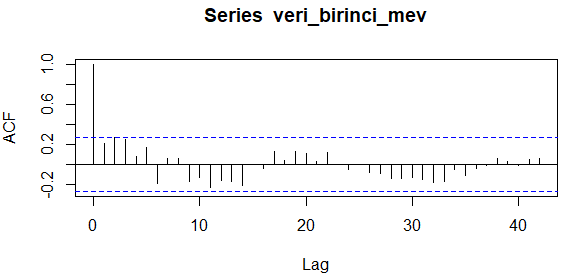
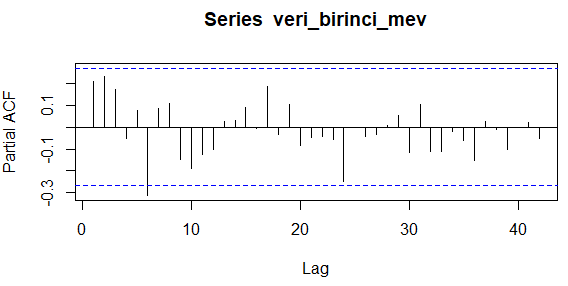
Birinci mevsimsel fark aldıktan sonraki ACF grafiğine bakıldığında mevsimselliğin bittiğini görüyoruz ve ayrıca PACF grafiğindeki 6. gecikmede bir değişme var gibi gözüküyor hem negatif sınıra geçmiş hemde gecikmenin boyutu küçülmüş bu bize periyodun doğru belirlendiğini gösteren işaretlerden biridir. Artık bu seri üzerinden gerekli çözümlemeler yapılabilir hale gelmiştir.
Şimdi ise hem trende hem mevsimselliğe sahip olan bir veride fark işlemleri nasıl yapılır onu gösterelim.
#Veri yükleme
data <- read_sav("C:/Users/asus/Desktop/DERSLER/İST477-ZAMAN DİZİLERİ ÇÖZÜMLEMESİ/1. hafta/I118.sav")
head(data)
#Zaman Serisi Grafiği plot.ts(data)
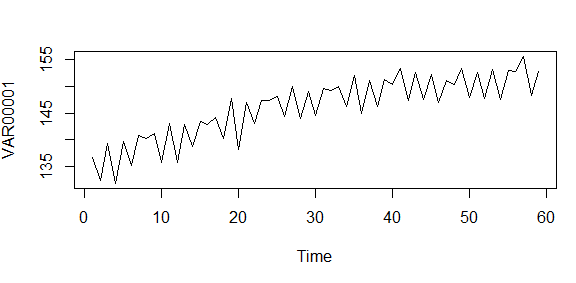
Yukarıdaki zaman serisi grafiğine baktığımızda, serinin artan bir trende ve dalgalanmalara sahip olduğu gözüküyor ama kesin bir sonuç için ACF ve PACF grafiklerine bakmamız gerekir.
#ACF, PACF Grafikleri ve Tabloları acf(data, lag.max = 42) data_acf_tablosu <- acf(data, lag.max = 42, plot = F) data_acf_tablosu pacf(data, lag.max = 42) data_pacf_tablosu <- pacf(data, lag.max = 42, plot = F) data_pacf_tablosu
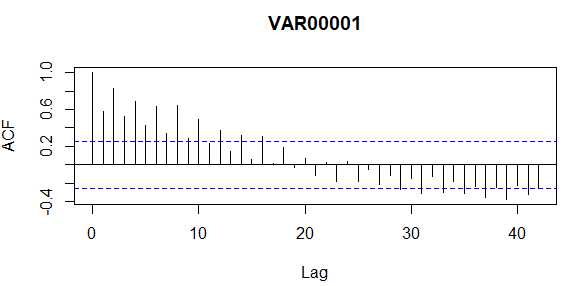
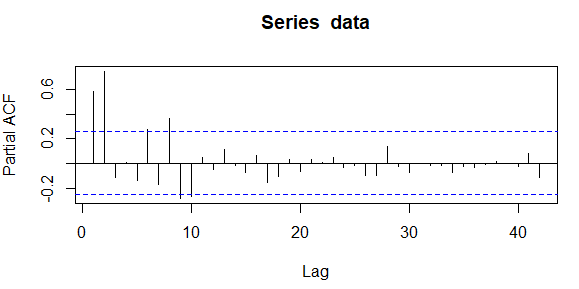
Yukarıdaki ACF grafiğine bakıldığında ilk 4 gecikme hatta daha fazlası sınırlar dışında olduğundan dolayı seri trende sahiptir bundan kurtulmak için 1. dereceden mevsimsel olmayan fark almamız lazım.
data_birinci_fark <- diff(data$VAR00001, differences = 1) acf(data_birinci_fark, lag.max = 42) #Mevsimsellik ağır basıyor mevsimsel fark almamız lazım periyot 8 pacf(data_birinci_fark, lag.max = 42)
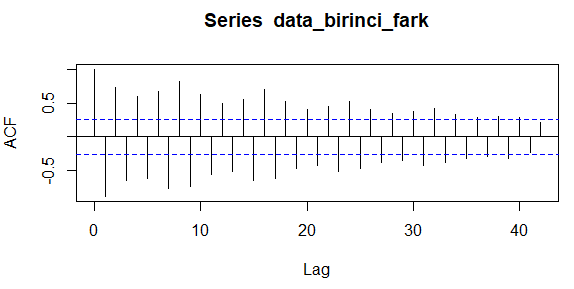
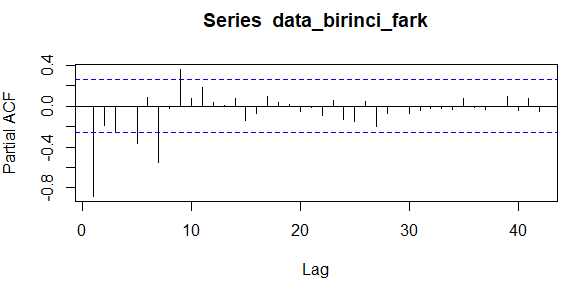
Birinci dereceden fark aldığımızda ACF grafiğinde dalgalanmalar olduğunu yani mevsimselliğin var olduğunu görüyoruz. Periyodu belirlediğimizde 8 olduğunu görüyoruz(En büyük ilk gecikmeden ikinci en büyük gecikmeye kadar). Ayrıca PACF’deki 8. gecikmenin de sınırlar dışarısında olduğunu görüyoruz. Periyot 8 olarak belirledikten sonra 1. dereceden mevsimsel fark alalım.
data_birinci_mev <- diff(data_birinci_fark,8) acf(data_birinci_mev,lag.max = 42) pacf(data_birinci_mev, lag.max = 42)
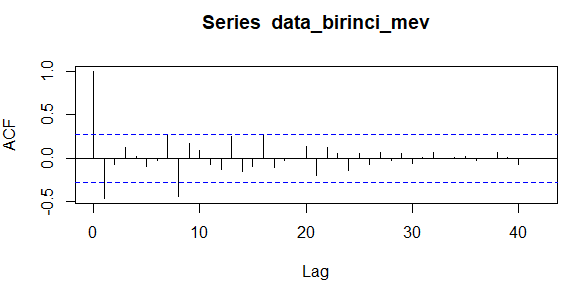
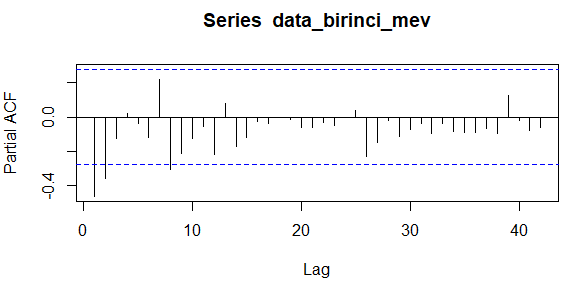
Mevsimsel farkı aldığımızda serinin durağanlaştığını görüyoruz. Seri durağan hale geldikten sonra artık bu seri üzerinden gerekli çözümlemeler yapılabilir hale gelmiştir.
Bu yazımızın sonuna gelmiş bulunmaktayız bir sonraki yazımızda görüşmek üzere 🙂
Saygılarımla..
Osman IŞIK