![]()
Giriş
Temel Bileşenler Analizi nedir? Nasıl hesaplanır? Faydaları nelerdir? Nasıl uygulanır? Bu soruların cevabı için doğru yerdesiniz.
Veri bilimi çalışmalarında çok sayıda değişkenle çalışılması gerekebilir. Bu durum; eğitim(training) süresinin fazla olması, aşırı öğrenme(overfitting) ve çoklu doğrusal bağlantı(multicollinearity) gibi çeşitli sorunları beraberinde getirir. Hazırlanan modellerin optimum sürede, optimum performansla çalışması gerekecektir. Ayrıca lojistik regresyon ve lineer regresyon gibi istatistiksel algoritmalarda çoklu doğrusal bağlantı sorunu çarpık ve yanıltıcı sonuçlara yol açabilir.
Bu problemleri aşmak için değişken seçimi (feature selection) ve boyut indirgeme (dimensionality reduction) yöntemleri kullanılabilir. Değişken seçiminde veri setindeki değişken korunur ya da tamamen kaldırılır. Boyut indirgemede ise mevcut değişkenlerin kombinasyonundan oluşan yeni değişkenler yaratılarak değişken sayısı azaltılır. Böylece veri setindeki tüm özellikler bir şekilde hala mevcut ancak değişken sayısı azaltılmış olur.
Birçoğumuzun analizlerde yaşadığı bu sorunları aşmak için en çok tercih edilen boyut indirgeme yöntemlerinden biri olan Temel Bileşenler Analizi’ni yakından inceleyelim.

TEMEL BİLEŞENLER ANALİZİ NEDİR? NASIL HESAPLANIR?
Temel Bileşenler Analizi; birbirleri ile ilişkili olan çok sayıda değişkenden meydana gelen bir çok değişkenli sistemi, bu değişkenlerin doğrusal fonksiyonları şeklinde daha az sayıda ve birbirleri ile ilişkisiz ve aynı zamanda önceki sisteme ait toplam değişimi mümkün olduğunca büyük oranda açıklayabilen yeni değişkenlerden meydana gelen sisteme dönüştüren çok değişkenli istatistiksel analiz tekniğidir. Analiz sonucunda oluşan her bir yeni değişkene temel bileşen denir.
Temel Bileşenler Analizi’nde p sayıda başlangıç değişkenine karşılık elde edilen p sayıda temel bileşenin her biri, orijinal değişkenlerin doğrusal bir bileşimidir. Dolayısıyla, her bir temel bileşen bünyesinde tüm değişkenlerden belirli oranda bilgiyi barındırır. Bu özelliği sayesinde Temel Bileşenler Analizi, p boyutlu veri kümesi yerine, ilk m önemli temel bileşenin kullanılması yoluyla boyut indirgemesi sağlayabilmektedir. İlk m temel bileşen toplam varyansın büyük kısmını açıklıyorsa, geriye kalan p-m temel bileşen ihmal edilebilir. Klasik değişken seçimi teknikleri ile karşılatırıldığında bu yöntem ile bilgi kaybı oldukça aza indirilecektir.
Temel Bileşenler Analizi uygulanırken bazı konulara özen gösterilmelidir. Veriye Temel Bileşenler Analizi uygulamadan önce mutlaka standardizasyon yapılmalıdır. Farklı ölçeklerdeki veriler yanıltıcı bileşenlere sebep olacaktır. Ayrıca analiz aykırı gözlemlerden(outlier) fazlaca etkilenir. Mutlaka analizden önce veriler aykırı gözlemlerden ayrılmalı ya da Randomized PCA, Sparse PCA gibi alternatif yöntemler kullanılmalıdır.
Temel bileşenler hesaplanırken sırasıyla aşağıdaki adımlar takip edilir.
- Her boyut için ortalama vektör hesaplanır.
- Kovaryans matrisleri hesaplanır.
- Her boyut için özvektörleri ve karşılık gelen özdeğerleri hesaplanır.
- Her bir özdeğerin özdeğerler toplamına bölünmesi ile temel bileşenlerin toplam varyansı açıklama yüzdeleri elde edilir.
Temel Bileşenler Analizi;
- Boyut indirgeme
- Verileri korelasyondan arındırma
- Yüksek boyutlu verilerin görselleştirilmesi
- Gürültü filtreleme
gibi çalışmalar için oldukça yararlıdır.
Konu ile ilgili Python uygulamasına 2. sayfadan ulaşabilirsiniz.
TEMEL BİLEŞENLER ANALİZİ PYTHON UYGULAMASI
Çalışmada “Human Activity Recognition” veri seti kullanılmıştır. 30 gönüllü denek ile oluşturulan bu veri setinde, gönüllülere akıllı telefonlar üzerlerindeyken yürüme, merdiven çıkma, merdiven inme, oturma, kalkma ve uzanma hareketleri yaptırılmıştır. Veri setinin amacı elde edilen verilerle insan davranışlarının tahminlenmesidir.
import pandas as pd import os import numpy as np import matplotlib.pyplot as plt import seaborn as sns from IPython.display import Image from warnings import filterwarnings
df = pd.read_csv('Simplified_Human_Activity_Recognition.csv')df.shape
(3609, 562)
Datada 3.609 satır ve 562 sütun bulunmaktadır.
y= df['activity']
X = df.iloc[:,1:]
X.head()
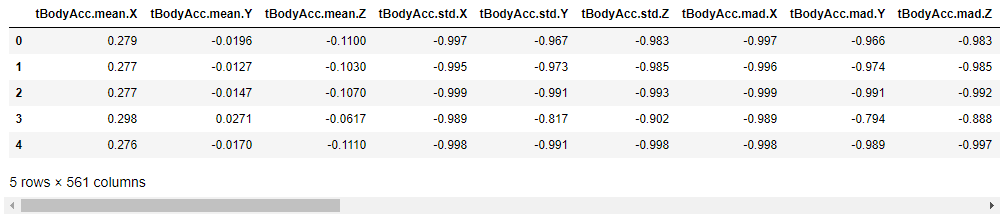
correlation_exp=X[['angle.X.gravityMean','angle.Y.gravityMean','tBodyAcc.std.X','tBodyAcc.std.Y',
'tBodyAcc.mad.X','tBodyAcc.std.X','tBodyAcc.min.Y','tBodyAcc.std.Y']]
# Korelasyon Matrisi
corr = correlation_exp.corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
f, ax = plt.subplots(figsize=(10, 8))
cmap = sns.diverging_palette(220, 10, as_cmap=True)
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=1, center=0,annot=True,
square=True, linewidths=.5, fmt= '.1f', cbar_kws={"shrink": .5})
plt.show()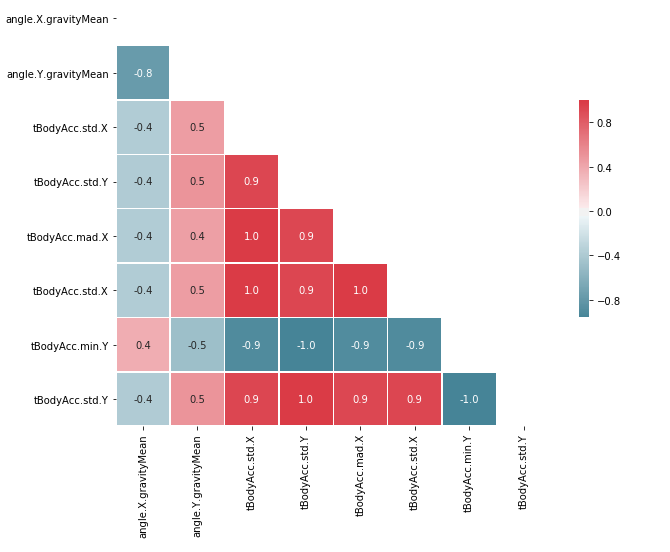
561 değişkenin korelasyon matrisinin incelemesinin zor olmasından dolayı örnek değişkenlerin korelasyon matrisi eklenmiştir. Görüldüğü gibi veri setinde çok yüksek korelasyona sahip değişkenler bulunmaktadır.
# Veriler 0 ile 1 aralığında ölçeklendirilmiştir from sklearn.preprocessing import MinMaxScaler features = X.columns.values scaler = MinMaxScaler(feature_range = (0,1)) scaler.fit(X) X = pd.DataFrame(scaler.transform(X)) X.columns = features
TEMEL BİLEŞENLERİN HESAPLANMASI
# Herbir Değişken için Ortalama Vektör Hesaplanmıştır mean_vec = np.mean(X, axis=0) #Kovaryans Matrisi cov_mat = (X - mean_vec).T.dot((X - mean_vec)) / (X.shape[0]-1) #Özvektörler ve Özdeğerlerin Hesaplanmıştır eig_vals, eig_vecs = np.linalg.eig(cov_mat) # Özdeğer ve özvektör başlıklarının tuple haline getirilmiştir eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))] # Tuple'lar sıralanmıştır eig_pairs.sort(key=lambda x: x[0], reverse=True) #Açıklanan Varyanslar ve Kümüle Varyans Hesaplanmıştır tot = sum(eig_vals) var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)] cum_var_exp = np.cumsum(var_exp) #Bileşenlerin Açıkladıkları Varyanslar(ilk 10) var_exp[:10]

#Kümülatif Açıklanan Varyans(ilk 10) cum_var_exp[:10]

plt.figure(figsize=(18, 10))
plt.bar(range(1,11), var_exp[:10], label='Bileşenin Açıkladığı Varyans', color='lightskyblue')
plt.step(range(1,11), cum_var_exp[:10], label='Kümülatf Açıklanan Varyans',color='red')
plt.ylabel('Açıklanan Varyans')
plt.xlabel('Temel Bileşenler')
plt.show()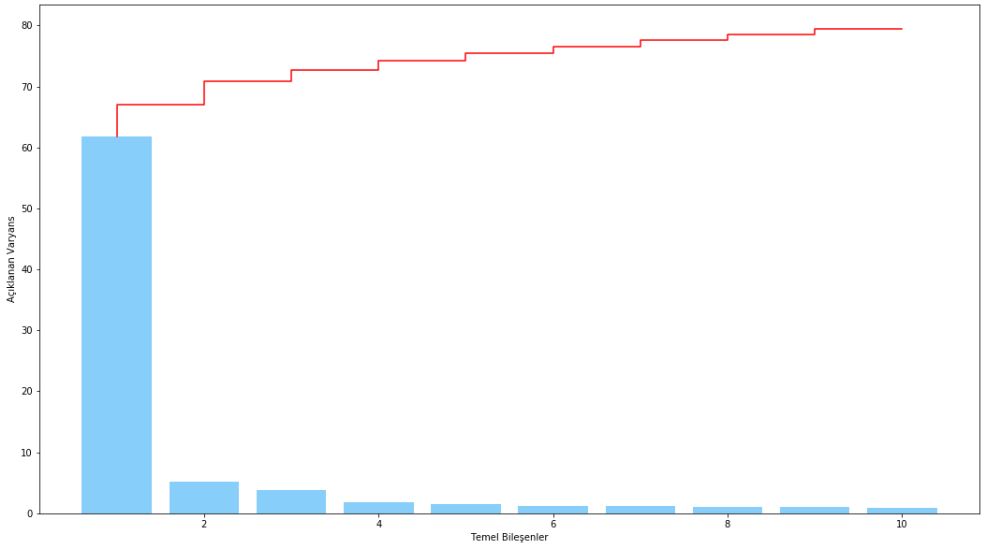
İlk bileşen toplam varyansın yarısından fazlasını açıklamaktadır. Daha fazla açıklayıcılığın olmasını istenebilir. Örneğin %75 açıklanan varyans ilk 5 değişken ile elde edilebilmektedir.
Kısa Yol
Önceki kodlarda analizin daha açıklayıcı olabilmesi adına ortalama vektör, kovaryans matrisi, özvektör ve özdeğerler hesaplanarak bileşenler elde edilmişti. Bundan sonraki bölümde ise analizlerde kullanmaya daha elverişli olan sklearn kütüphanesi kullanılacaktır.
from sklearn.decomposition import PCA pca = PCA(n_components=561) X_PCA = pca.fit_transform(X) explained_variance = pca.explained_variance_ratio_
#PCA değerleri dataya eklenmiştir
for i in range (1,6):
df['PCA_%s' %i] = X_PCA[:, i]İlk 5 bileşen toplam varyansın %75’ini kapsamaktadır.
X = df.iloc[:,562:] X.head()

corr = X.corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
f, ax = plt.subplots(figsize=(8,6))
cmap = sns.diverging_palette(220, 10, as_cmap=True)
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=1, center=0,annot=True,
square=True, linewidths=.5, fmt= '.1f', cbar_kws={"shrink": .5})
plt.show()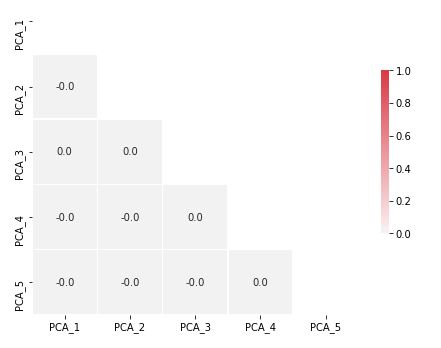
Tabloda görüldüğü üzere bileşenler arasında korelasyon yoktur.
LOJISTIK REGRESYON
#Veri seti %70 train, %30 test olarak bölünmüştür from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.30, random_state = 42) from sklearn.linear_model import LogisticRegression loj = LogisticRegression(solver = "liblinear") loj_model = loj.fit(X_train,y_train) print(loj_model.score(X_test,y_test))
0.7608494921514312
Model %76 accuracy ile tahminleme yapmıştır.
BİLEŞENLERİN GRAFİKSEL GÖSTERİMİ
actvity=df['activity']
data_for_graph = pd.concat([X,actvity],axis=1)
markers = [1,2,3,4,5,6]
sns.pairplot(data_for_graph, hue = 'activity', markers = markers, height=5, plot_kws={"s": 25});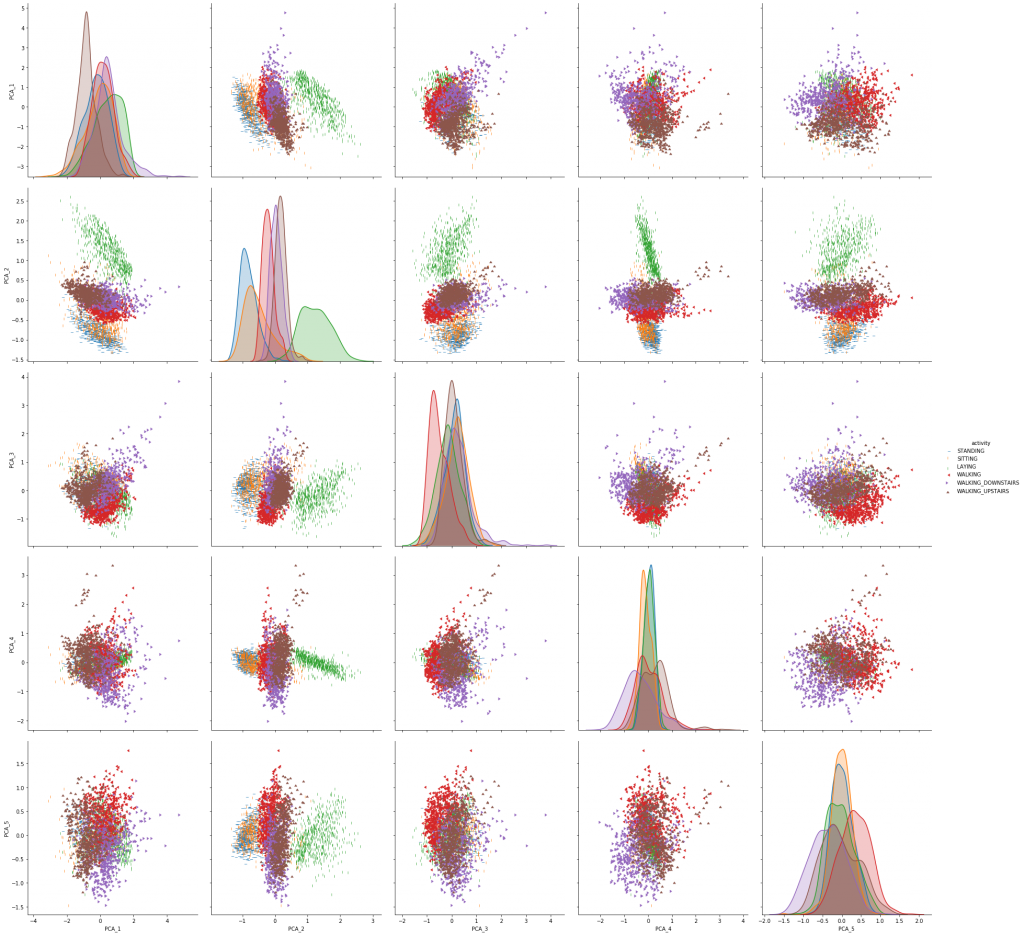
Temel bileşenlerden oluşan scatter plot incelendiğinde beklenen sonuçlar elde edilmiştir. Yeşil ile gösterilen uzanma hareketinin diğer hareketlerden ayrışmış; kırmızı, mor ve kahverengiyle gösterilen yürüme, merdiven çıkma ve merdiven inme hareketleri ise birbiri ile benzerlik göstermiştir.
SONUÇ
Çalışmada öncelikle detaylı şekilde Temel Bileşenlerin nasıl hesaplandığı sonrasında sklearn kütüphanesi ile hızlı bir şekilde nasıl kullanılabileceği gösterilmiştir. Çalışma sonucunda aralarında yüksek korelasyona sahip verilerin bulunduğu 561 bağımsız değişkenden, korelasyon sorunu olmayan ve tüm datanın %75’ini açıklayabilen 5 bileşenden oluşan yeni veri seti hazırlanmış ve lojistik regresyon algoritması ile modellenmiştir. Korelasyon sorununu çözerek modelde olası çoklu doğrusal bağlantı sorununun önüne geçilmiş ve değişken sayısı azaltılarak training süresinin kısaltılmış ve overfitting riskinin azalması sağlanmıştır.
KAYNAKLAR
- Veri Zarflama Analizinde Temel Bileşenler Analizinin Kullanımı — Seda Sütçü Asar (Yüksek Lisans Tezi)
- Türkiyede İllerin Ekonomik Performanslarinin Veri Zarflama Analizi Ve Temel Bileşenler Analizi Yöntemleri ile Değerlendirilmesi – Burçin Öner (Yüksek Lisans Tezi)
- Temel Bileşenler Analizi için Robust Algoritmaları – Aysu Özen Yaycili (Yüksek Lisans Tezi)
- Principal Components in the Problem Of Multicollineartity – Neslihan Ortabaş (Yüksek Lisans Tezi)
- Principal Components to Overcome Multicollinearity Problem – Abubakari S.Gwelo (Makale)
- https://medium.com/datadriveninvestor/principal-components-analysis-pca-71cc9d43d9fb
- https://medium.com/@davidstroud/principal-components-analysis-pca-9d97571a0e91
- https://www.kaggle.com/nirajvermafcb/principal-component-analysis-explained
- Veri seti: https://www.kaggle.com/mboaglio/simplifiedhuarus