
![]()
Utku Kubilay ÇINAR
Beni çok etkileyen bir söz ile yazıma başlamak isterim. Görselde gördüğünüz “Voyager 2” uzay aracıdır. Güneş sisteminin dışına gönderilen, insanlık tarihinin en büyük keşif projesidir. Bu yazıda Keşifçi Veri Analizi örnek uygulaması yapılacaktır.
“Mikroskop insana ne kadar önemli olduğunu gösterdi; teleskop ise ne kadar önemsiz olduğunu…” –Manly P.Hall
Veri biliminde, keşifçi veri analizi bilindiği üzere önemli bir başlıktır. Bu yazımda bazı keşifçi veri analizi yöntemleri ile kısa bir inceleme yapacağız. Türkiye’deki bazı akarsuların bileşenlerini yani suların analizini yapacağız ve hangi bölgelerde hangi fabrikalar var, hangi fabrikada kaçıncı seviye arıtma tesisi var ve bunlar suyun kalitesini ve içeriğini nasıl etkiliyor ? Bu gibi soruların cevaplarını arayacağız.
Bu yazının temel amacı, keşifçi veri analizlerinin önemini göstermek ve kısa bir çalışma ile ne gibi sonuçlar görebileceğimizi irdelemektir. Veri bilimciler olarak bizlerin temel görev ve sorumlulukları arasında veriyi modellemek, algoritmalar ile sorunu çözmek gibi maddeler olsa da keşifçi veri analizleri ile mevcut sorunları göstermek ve bu sorunları çözmek için öneriler de sunmak olduğunu unutmamalıyız.
Analizlerimize başlayabiliriz.
Kullanılan Kütüphaneler(Pokemonlar)
library(haven) # veriyi yükleme library(DataExplorer) # Keşifçi veri analizi library(DT) #çıktıyı tablo halinde görüntüleyebilme library(RcmdrMisc) # yardımcı tools library(Boruta) # Parametre Önemi için yaygın olarak kullanılan algoritmalardan biri (Feature Selection) library(tidyverse) # Veri manipülasyonu library(colorspace) library(data.table)
Veri Setini Yükleme
ornekdata <- read_sav("C:/Users/user/Desktop/örnekdata.sav")
options(warn = -1)Veri setini R Studio 3.5.0 programına yükledikten sonra veri setini ve parametrelerini inceleyelim.
head(ornekdata)
## # A tibble: 6 x 52 ## H_KOD ISTNO ISTAD kodil İlgrup IL ORNNOK MVCBSK IZLKOOR_X IZLKOOR_Y ## <dbl> <chr> <chr> <dbl> <dbl> <chr> <chr> <chr> <dbl> <dbl> ## 1 1 SU-1 Sima~ 1 2 Kuta~ Simav~ Kisme~ NA NA ## 2 1 SU-2 Sima~ 1 2 Kuta~ Simav~ Yün y~ NA NA ## 3 1 SU-3 Sima~ 2 2 Bali~ Arnav~ Tarim~ NA NA ## 4 1 SU-4 Sima~ 2 2 Bali~ Cayir~ Tarim~ NA NA ## 5 1 SU-5 Sima~ 2 2 Bali~ Sindi~ Mezba~ NA NA ## 6 1 SU-6 Nerg~ 2 2 Bali~ Balik~ OSB, ~ NA NA ## # ... with 42 more variables: IZLTYPE <dbl+lbl>, SCKLK <dbl>, pH <dbl>, ## # CO <dbl>, EC <dbl>, OD <dbl>, CL <dbl>, SO4 <dbl>, NH4_N <dbl>, ## # NO2_N <dbl>, NO3_N <dbl>, TP <dbl>, TÇM <dbl>, Na <dbl>, KOI <dbl>, ## # TKN <dbl>, BOI <dbl>, YG <dbl>, MBAS <dbl>, Hg <dbl>, Cd <dbl>, ## # Pb <dbl>, As <dbl>, Cu <dbl>, T_Cr <dbl>, CR_6 <dbl>, COB <dbl>, ## # Ni <dbl>, Zn <dbl>, TCn <dbl>, F <dbl>, SCI <dbl>, S <dbl>, Fe <dbl>, ## # Mn <dbl>, B <dbl>, Se <dbl>, Ba <dbl>, Al <dbl>, FKOL <dbl>, ## # TKOL <dbl>, Pt_Co <dbl>
Veri setinde de görüldüğü gibi, suların bileşenlerini ve örnek alınan nehrin bazı özelliklerini içeren bir veri seti olduğunu görüyoruz.
Bir içme suyunun “kaliteli” olarak adlandırılabilmesi için bazı bileşenlerin belli oranlarda olması gerekmektedir. Su tadını, rengini ve kokusunu bu gibi bileşenlerinden alır.
names(ornekdata)
## [1] "H_KOD" "ISTNO" "ISTAD" "kodil" "İlgrup" ## [6] "IL" "ORNNOK" "MVCBSK" "IZLKOOR_X" "IZLKOOR_Y" ## [11] "IZLTYPE" "SCKLK" "pH" "CO" "EC" ## [16] "OD" "CL" "SO4" "NH4_N" "NO2_N" ## [21] "NO3_N" "TP" "TÇM" "Na" "KOI" ## [26] "TKN" "BOI" "YG" "MBAS" "Hg" ## [31] "Cd" "Pb" "As" "Cu" "T_Cr" ## [36] "CR_6" "COB" "Ni" "Zn" "TCn" ## [41] "F" "SCI" "S" "Fe" "Mn" ## [46] "B" "Se" "Ba" "Al" "FKOL" ## [51] "TKOL" "Pt_Co"
Veri setindeki parametre isimlerine bakıldığında görüldüğü üzere veri setinde siyanür ve arsenik gibi zehir bileşenleri de bulunmaktadır. Bu değişkenler ile kaliteli bir su ayrımı yapılabilir. Kümeleme yöntemleri ile akarsuları birbirinden ayırabiliriz. Korelasyonlarını inceleyebiliriz. Önemli bileşenlerin birbirini nasıl etkilediğini öğrenebiliriz. Başka keşifçi analizler de yapılabilir fakat yazıyı uzun tutmak istemiyorum ve yapılabilecek diğer analiz ve yöntemleri de sizlere bırakıyorum.
Veri Manipülasyonu
Analizlerimize ve keşifçi veri analizine başlamadan önce veri setini, analizlere uygun hale getirmek gerekmektedir. Öncelikle eksik gözlem incelemesi yapılmıştır.
Eksik ya da kayıp gözlemler incelenmiştir.
plot_missing(ornekdata, title = "Kayıp Veriler")

IZLKOOR_x ve IZLKOOR_Y değişkenlerinde bir değer olmadığı için veri setinden çıkarılmıştır. Diğer eksik gözlemler ise grafikte de görüldüğü gibi kabul edilebilir seviyededir.
ornekdata <- ornekdata %>% select(-IZLKOOR_X, -IZLKOOR_Y, -ISTNO, -ORNNOK, -MVCBSK, -FKOL,-CR_6,-Hg) # Veri setinden çıkarma işlemi
Veri setimizdeki bileşenlerin özet bilgisi;
summary(ornekdata) # Özet istatistikler
## H_KOD ISTAD kodil İlgrup ## Min. :1.000 Length:58 Min. :1.000 Min. :1.000 ## 1st Qu.:1.000 Class :character 1st Qu.:3.000 1st Qu.:1.000 ## Median :3.000 Mode :character Median :4.000 Median :2.000 ## Mean :2.845 Mean :4.638 Mean :1.655 ## 3rd Qu.:4.000 3rd Qu.:6.000 3rd Qu.:2.000 ## Max. :5.000 Max. :9.000 Max. :2.000 ## ## IL IZLTYPE SCKLK pH ## Length:58 Min. :1.0 Min. : 7.40 Min. :7.190 ## Class :character 1st Qu.:1.0 1st Qu.:12.05 1st Qu.:7.782 ## Mode :character Median :1.5 Median :13.95 Median :7.910 ## Mean :1.5 Mean :14.06 Mean :8.011 ## 3rd Qu.:2.0 3rd Qu.:15.28 3rd Qu.:8.160 ## Max. :2.0 Max. :23.00 Max. :9.310 ## ## CO EC OD CL ## Min. : 0.870 Min. : 107 Min. : 8.30 Min. : 0.00 ## 1st Qu.: 2.607 1st Qu.: 603 1st Qu.: 27.57 1st Qu.: 28.25 ## Median : 4.330 Median : 939 Median : 43.00 Median : 55.50 ## Mean : 4.968 Mean :1189 Mean : 49.06 Mean : 163.49 ## 3rd Qu.: 7.242 3rd Qu.:1155 3rd Qu.: 70.10 3rd Qu.: 161.25 ## Max. :11.000 Max. :6440 Max. :111.00 Max. :1410.00 ## ## SO4 NH4_N NO2_N NO3_N ## Min. : 12.0 Min. : 0.0000 Min. :0.0000 Min. :0.000 ## 1st Qu.: 66.0 1st Qu.: 0.5125 1st Qu.:0.1113 1st Qu.:0.625 ## Median : 95.5 Median : 2.8500 Median :0.1945 Median :1.300 ## Mean :126.0 Mean : 3.9948 Mean :0.3482 Mean :1.322 ## 3rd Qu.:156.5 3rd Qu.: 5.8750 3rd Qu.:0.3025 3rd Qu.:2.000 ## Max. :440.0 Max. :14.7000 Max. :7.3400 Max. :4.500 ## ## TP TÇM Na KOI ## Min. :0.0000 Min. : 175.0 Min. : 1.50 Min. : 0.0 ## 1st Qu.:0.4025 1st Qu.: 389.5 1st Qu.: 28.00 1st Qu.: 21.0 ## Median :0.7250 Median : 539.5 Median : 50.00 Median : 42.5 ## Mean :1.0128 Mean : 735.3 Mean : 60.88 Mean : 84.9 ## 3rd Qu.:1.1950 3rd Qu.: 743.8 3rd Qu.: 74.40 3rd Qu.:102.2 ## Max. :4.2900 Max. :3606.0 Max. :202.00 Max. :815.0 ## ## TKN BOI YG MBAS ## Min. : 0.000 Min. : 0.000 Min. : 0.00 Min. :0.0000 ## 1st Qu.: 2.325 1st Qu.: 0.000 1st Qu.: 0.00 1st Qu.:0.0000 ## Median : 7.730 Median : 0.000 Median : 1.01 Median :0.5000 ## Mean :10.650 Mean : 9.121 Mean :10.24 Mean :0.6467 ## 3rd Qu.:16.000 3rd Qu.: 10.000 3rd Qu.:19.00 3rd Qu.:1.1475 ## Max. :45.250 Max. :210.000 Max. :48.00 Max. :2.0000 ## NA's :5 ## Cd Pb As Cu ## Min. :0.0000 Min. : 0.00 Min. : 0.00 Min. : 0.00 ## 1st Qu.:0.0000 1st Qu.: 0.00 1st Qu.: 0.00 1st Qu.: 0.00 ## Median :1.0000 Median : 0.00 Median : 4.00 Median : 3.00 ## Mean :0.7414 Mean : 11.17 Mean : 21.69 Mean : 18.02 ## 3rd Qu.:1.0000 3rd Qu.: 0.00 3rd Qu.: 28.75 3rd Qu.: 17.00 ## Max. :6.0000 Max. :294.00 Max. :256.00 Max. :256.00 ## ## T_Cr COB Ni Zn ## Min. : 0.00 Min. : 0.000 Min. : 0.00 Min. : 1.00 ## 1st Qu.: 0.00 1st Qu.: 0.000 1st Qu.: 4.00 1st Qu.: 7.50 ## Median : 3.50 Median : 0.000 Median : 7.00 Median : 17.50 ## Mean : 14.76 Mean : 1.448 Mean : 15.07 Mean : 121.00 ## 3rd Qu.: 15.75 3rd Qu.: 0.000 3rd Qu.: 12.00 3rd Qu.: 77.75 ## Max. :118.00 Max. :36.000 Max. :155.00 Max. :2177.00 ## ## TCn F SCI S ## Min. : 0.000 Min. : 0.0 Min. : 20.0 Min. : 0.0 ## 1st Qu.: 0.000 1st Qu.: 0.0 1st Qu.: 102.5 1st Qu.: 0.0 ## Median : 0.000 Median : 0.0 Median : 190.0 Median : 25.0 ## Mean : 1.483 Mean : 122.8 Mean : 299.3 Mean : 94.1 ## 3rd Qu.: 0.000 3rd Qu.: 177.5 3rd Qu.: 372.5 3rd Qu.: 123.2 ## Max. :63.000 Max. :1880.0 Max. :1330.0 Max. :1714.0 ## ## Fe Mn B Se ## Min. : 18.0 Min. : 4.0 Min. : 31.0 Min. : 0.0 ## 1st Qu.: 192.8 1st Qu.: 118.5 1st Qu.: 196.8 1st Qu.: 0.0 ## Median : 469.0 Median : 212.0 Median : 406.5 Median : 0.0 ## Mean : 967.9 Mean : 367.5 Mean : 622.8 Mean : 5.0 ## 3rd Qu.:1105.8 3rd Qu.: 310.5 3rd Qu.: 629.2 3rd Qu.:14.5 ## Max. :6924.0 Max. :6140.0 Max. :3436.0 Max. :25.0 ## ## Ba Al TKOL Pt_Co ## Min. : 17.00 Min. :0.0000 Min. : 0 Min. : 0.00 ## 1st Qu.: 64.75 1st Qu.:0.0700 1st Qu.: 0 1st Qu.: 29.50 ## Median : 99.50 Median :0.2015 Median : 1150 Median : 49.00 ## Mean :113.57 Mean :0.7226 Mean : 3836 Mean : 85.05 ## 3rd Qu.:128.75 3rd Qu.:0.8170 3rd Qu.:10000 3rd Qu.:112.50 ## Max. :721.00 Max. :7.8800 Max. :10000 Max. :347.00 ##
Özet istatistikler incelendiğinde illerin kodları, grupları, bulundukları nehir ya da çayın isimleri gibi lokasyon bilgileri de mevcuttur.
Analizlerde kullanılacak olan parametrelerin karakterleri incelenmiştir.
Gruplandırma yapabileceğimiz değişkenleri faktör olarak atama yapıyoruz.
ornekdata$H_KOD <- as.factor(ornekdata$H_KOD) ornekdata$ISTAD <- as.factor(ornekdata$ISTAD) ornekdata$kodil <- as.factor(ornekdata$kodil) ornekdata$İlgrup <- as.factor(ornekdata$İlgrup) ornekdata$IZLTYPE <- as.factor(ornekdata$IZLTYPE)
İllere göre gruplandırma yapacağımız zaman İzmir ilinde bazı değişkenler ilçeleri ile beraber yazıldığı için bu değerleri, “İzmir” olarak güncel hali ile yazmak gerekmektedir. Böylece İzmir ilinin gerçek değeri görülebilir.
ornekdata$IL[which(ornekdata$IL %in% c("Izmir/Selcuk","Izmir/Beydag","Izmir/Tire", "Izmir"))] <- "İzmir"
ornekdata %>% group_by(IL) %>% summarise(Nehir_Sayısı=n()) %>% arrange(desc(Nehir_Sayısı))## # A tibble: 9 x 2 ## IL Nehir_Sayısı ## <chr> <int> ## 1 İzmir 13 ## 2 Manisa 10 ## 3 Balikesir 8 ## 4 Bursa 7 ## 5 Tekirdag 6 ## 6 Kirklareli 4 ## 7 Kutahya 4 ## 8 Edirne 3 ## 9 Usak 3
ornekdata$IL <- as.factor(ornekdata$IL)
Görüldüğü üzere veri setimizde en çok verisi bulunan şehirlerimiz sırasıyla İzmir, Manisa ve Balıkesir’dir.
Görsel İnceleme
plot_bar(ornekdata[-c(1,3)])

Şeklindedir. Bu değişkenler ile gruplandırma işlemleri(group_by() fonksiyonu ile) yapılabilir ve bu parametreler faktör olarak atama yapıldığında ayrı başlık olarak incelenebilir.
Histogramları ve Dağılımları İncelediğimizde
plot_histogram(ornekdata)



Bileşenlerin dağılımı şekilde görüldüğü gibidir. Bu grafikleri incelemek, keşifçi veri analizinde önemli yere sahiptir.
Boxplot İncelemesi
Bazı önemli parametrelerde uç değerlerin olduğu gözlemlenmiştir.
par(mfrow=c(3,2)) boxplot(ornekdata$pH, horizontal = T, main="pH") boxplot(ornekdata$CO, horizontal = T, main="CO") boxplot(ornekdata$SCKLK, horizontal = T, main="Sıcaklık") boxplot(ornekdata$EC, horizontal = T, main="EC") boxplot(ornekdata$OD, horizontal = T, main="OD") boxplot(ornekdata$SO4, horizontal = T, main="SO4")
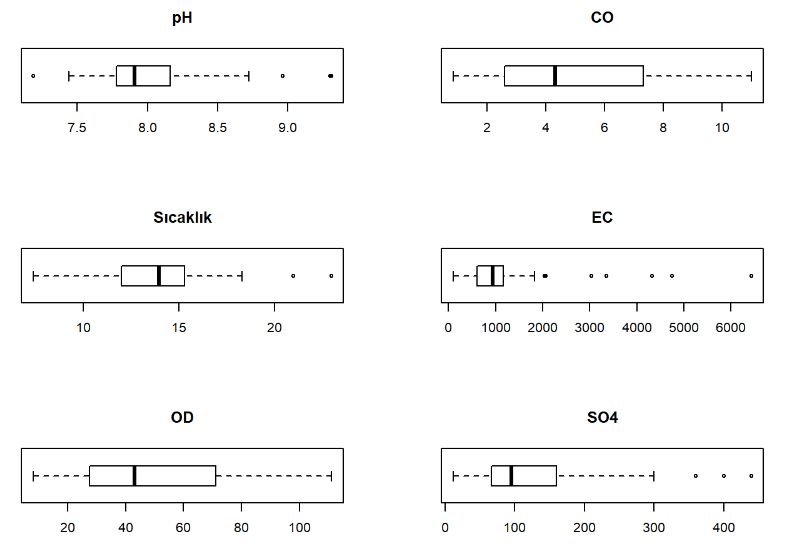
Görseller incelendiğinde bazı değişkenlerde uç değerler olduğu gözlemlenmiştir fakat veri seti detaylı incelendiğinde ve veri setinin yani akarsuların karakterleri incelendiğinde bu uç değerlerin ölçüm hatası ya da verinin yanlış girilmesi gibi bir durumun olmadığı anlaşılmıştır. Uç değerlerin bizlere bir şey dediğini ve anlam içerdiği görülmelidir.
Bu uç değerlerin olmasının sebebi, ölçümün yapıldığı havzada arıtma tesisinin olmaması ya da o bölgede fabrikaların bulunmasıdır(Orjinal veri setinde akarsuların bulunduğu bölgede arıtma tesisinin varlığı ve çapı, bölgede bulunan fabrikalar gibi text formatında bilgiler de mevcuttur fakat analizlerin gösteriminde yer yerilmemiştir).
Bu detaylı inceleme yapılmasaydı ve uç değer olarak direk veri setinden silinseydi verinin bize söylemek istediği bilgileri anlayamayacaktık. Bu sebeple veri setinizde uç değerler varsa biraz durup sebebini anlamak gerekmektedir. Keşifçi veri analizinde, verinin bize söylemek istediği bilgileri algılamak ve görmek olduğu unutulmamalıdır.
Korelasyon İncelemesi
Korelasyonlar %95 güven düzeyinde anlamsız olanlar silinmiştir.
korelasyon_tablosu <- ornekdata %>% select(-ISTAD, -kodil, -IL, -H_KOD, -İlgrup, -IZLTYPE) plot_correlation(korelasyon_tablosu)

İçilebilir Suda pH Seviyesinin İncelenmesi
Araştırmalar ve literatür taraması sonucunda içilebilir suda bazı parametrelerin olmadığı(zehirli maddeler gibi) ve olması gereken parametrelerinde normal seviyede olduğu varsayımı altında incelendiğinde pH seviyesinin önemli parametrelerden biri olduğu görülmüştür. Literatürden de bu bilgi öğrenildikten sonra araştırmalarımız pH üzerine odaklanmıştır.
Bunun üzerine pH seviyesinin önemini anlamamızda ve gelecekte kuracağımız modelde pH seviyesini etkileyebilecek en önemli parametreler incelenmiştir.
Veri biliminde, çok boyutlu ve çok değişkenli veri setleri ile uğraştığımız için parametre seçimi(feature selection) çok önemli bir adımdır. Her değişken, bağımlı değişkeni aynı oranda etkilemez, bazıları daha önemlidir. Boruta algoritması ile bu önem belirlenebilir, büyük ölçekli veri setlerinde en önemli değişkenler kullanıbilir.
pH için Parametre Önemi
Parametre seçimi, Boruta Algoritması ile yapılmıştır. Parametre önemi sadece pH için değil diğer değişkenler için de hesaplanmıştır. Renk, koku ve sıcaklığa göre incelenmiştir fakat bu yazıda örnek olarak sadece pH gösterilmiştir.
par(mfrow= c(1,1)) plot(parametre_onemi_pH, main = "pH için Parametre Önemi ve Önem Sırası CO,OD,Mn,CL,NH4_N,Pt_Co,Zn,TÇM,TP,SCI")

Grafik incelendiğinde, pH seviyesini etkileyen en önemli bileşenler Çözünmüş Oksijen, Oksijen Doygunluğu, Mangan, Klorür ve Amanyum Azotu olarak sayılabilir.
Tablo olarak incelendiğinde, gerekli değerler aşağıdaki gibidir;
boruta.df_ph <- attStats(parametre_onemi_pH) # pH için datatable(boruta.df_ph)

Bu çıktı ile “meanImp” değişkenini büyükten küçüğe göre sıralandığında, bağımlı değişken üzerinde açıklayıcılığı en yüksek değişkenler görülebilir.
pH Üzerinde Etkili Bileşenler
ph_onem <- ornekdata %>% select(CO, OD, Mn, CL, NH4_N)
etiket <- ornekdata[,8]
etiket_renkler <- rev(rainbow_hcl(3))
pairs(ph_onem, col=etiket_renkler,
lower.panel = NULL,
cex.labels=2,
pch=3, cex=1 )
Grafikte görüldüğü gibi bileşenler arasında ilişki mevcuttur. Bazı bileşenler, bazı bileşenlerle tepkimeye girerek farklı sonuçlar elde edebilir. Bu durum incelemeye açıktır.
Paralel koordinat grafiği ile hangi bileşenin diğerleri karşısında nasıl bir davranış sergilediği incelenmiştir.
library(MASS)
par(las = 1, mar = c(4.5, 3, 3, 2) + 0.1, cex = .8)
parcoord(ph_onem, col = etiket_renkler, var.label = TRUE, lwd = 2)
title("pH için önemli bileşenlerin paralel kordinat grafiği")
Grafiğe göre Mn bileşeni diğer bileşenlere göre azalma davranışı içindeyken bir örnekte bu durum tam tersidir(ilerleyen kısımlarda bu örnek incelendiğinde arsenik etkisi olduğu anlaşılmıştır).
Sıcaklığın İllere Göre Ortalama Değişimi
ggplot(ornekdata, aes(IL, SCKLK)) + geom_boxplot() + stat_summary(fun.y = mean,geom="point", shape=20, size=5, color="red", fill="red")

Grafikte kırmızı olarak gördüğümüz noktalar o ilde bulunan akarsuların sıcaklık ortalamalarıdır. Bu sıcaklıklar illere göre farklılık göstermektedir. Yazının ilerleyen kısımlarında pH seviyesinin ya da diğer seviyelerin illere göre grafikleri incelenecektir ve yapacağımız yorumların istatistiksel olarak anlamlı olup olmadığını anlamamız için ortalamaların istatistiksel testlerle kıyaslanması gerekmektedir. Bu testler %95 güven aralığında yapılmıştır.
Ortalamalar Arasındaki Farkın İncelenmesi
Homojenlik testi yapıldığında, varyansların homojen olması halinde yapılacak testler arasında genellikle “Tukey” testi tercih edilir.
Anova testinin varsayımlarından olan homojenlik testi incelendiğinde;
leveneTest(SCKLK~IL, data = ornekdata)
## Levene's Test for Homogeneity of Variance (center = median) ## Df F value Pr(>F) ## group 8 1.6901 0.1247 ## 49
p değerimizin % 95 güven aralığında incelendiğinde varyanslar eşit diyebiliriz. (sig. değeri > 0.05)
anova_test <- ornekdata %>% group_by(IL) %>% summarise(toplam = n(), ortalama = mean(SCKLK, na.rm = T), standart_sapma = sd(SCKLK, na.rm = T)) ornekdata %>% group_by(IL) %>% summarise(toplam = n(), ortalama = mean(SCKLK, na.rm = T), standart_sapma = sd(SCKLK, na.rm = T))
## # A tibble: 9 x 4 ## IL toplam ortalama standart_sapma ## <fct> <int> <dbl> <dbl> ## 1 Balikesir 8 13.9 1.81 ## 2 Bursa 7 15 2.77 ## 3 Edirne 3 14.6 0.723 ## 4 İzmir 13 13.9 1.34 ## 5 Kirklareli 4 15.7 3.06 ## 6 Kutahya 4 9.4 1.83 ## 7 Manisa 10 13.6 1.59 ## 8 Tekirdag 6 17.5 3.89 ## 9 Usak 3 11.2 0.173
Verilerin dağılımına bakıldığında normal ya da normale yakın olduğu görülmüştür. Veri sayısını arttırdığımızda Merkezi Limit Teoremi gereği normale yakınsayacaktır. Normallik varsayımı altında yapılan ortalamalar arasındaki farkların anlamlılığı incelendiğinde;
res.aov <- aov(SCKLK~IL, data = ornekdata) summary(res.aov)
## Df Sum Sq Mean Sq F value Pr(>F) ## IL 8 203.8 25.472 5.469 6.04e-05 *** ## Residuals 49 228.2 4.658 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Ho: Ortalamalar arasında fark yoktur.
H1: En az iki ortalama arasında anlamlı bir farklılık vardır.
Çıktımızdaki p değerine bakıldığında % 95 güven aralığında Ho hipotezi reddedilir ve ortalamalar arasında anlamlı bir farklılık olduğu söylenir. Sıcaklık iller bazında istatistiksel olarak anlamlı bir farklılık göstermektedir.
pH Seviyesinin İllere Göre Ortalama Değişimi
ggplot(ornekdata, aes(IL, pH)) + geom_boxplot() + stat_summary(fun.y = mean,geom="point", shape=20, size=5, color="red", fill="red") #pH

Oksijen Doygunluğunun İllere Göre Ortalama Değişimi
ggplot(ornekdata, aes(IL, CO)) + geom_boxplot() + stat_summary(fun.y = mean,geom="point", shape=20, size=5, color="red", fill="red") #oksijen doygunluğu
Suda Bulunan En Zehirli Maddelerin Başında Olan Arsenik
ggplot(ornekdata, aes(IL, As)) + geom_boxplot() + stat_summary(fun.y = mean,geom="point", shape=20, size=5, color="red", fill="red") # arsenik

İstatistiksel olarak anlamlı bileşenler grafiklerde gösterilmiştir. pH seviyesi en yüksek olan ilimiz Kütahya olmuştur. Aynı zamanda sıcaklık olarak en düşük ilimiz de Kütahya olmuştur. Bunun gibi yorumlar ve çıkarımlar çoğaltılabilir.
Sınıflandırma – Knn Algoritması
En yakın k-komşuluk ile veri setinde gruplandırma yapılmıştır.
library(cluster) ornekdata.standarize <- scale(na.omit(ornekdata[,7:44])) k.means.fit <- kmeans(ornekdata.standarize , 3) knn_siniflandirma <- mutate(na.omit(ornekdata), grup = k.means.fit$cluster)
Görselimiz,
clusplot(ornekdata.standarize, k.means.fit$cluster, main='Kümeleme',
color=TRUE, shade=TRUE,
labels=2, lines=0)
Grafik incelendiğinde zehirli maddelerin ve pH değerlerinin gruplandırmada önemli olduğu görülmüştür ve ayrılmıştır. Bu sınıflandırma ile suların kalitesine göre derecelendirme yapabiliriz. Gruplar incelendiğinde Arseniğin çok büyük etkisi olduğu görülmüştür. Arsenik oranına göre kaliteleri ölçeklendirilebilir.
res.aov.kume <- aov(grup~As, data = knn_siniflandirma) summary(res.aov.kume)
Df Sum Sq Mean Sq F value Pr(>F) As 1 5.753 5.753 42.13 3.47e-08 *** Residuals 51 6.964 0.137 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Kümelemelere ayırdıktan sonra veri setimizde, gruplar arasında anlamlı bir farkın olup olmadığını araştırmamız gerekmektedir(arsenik incelenmiştir çünkü grupların oluşturulmasında en etkili bileşen Arsenik olduğunu gördük). ANOVA Testi ile amaçlanan ise, değişkenlerin kümeler bazında anlamlı bir farklılık oluşturup oluşturmamasıdır. Gruplandırma işleminden sonra araştırmacının arzu ettiği çıktı ise gruplar arasında anlamlı bir farklılığın oluşmasıdır. Kümeleme analizlerinde, kümeler arasındaki uzaklık maksimum yapılır(bakınız diskriminant analizi).
En zehirli maddelerin başında gelen Arseniğe göre grafik oluşturduğumuzda;
ggplot(knn_siniflandirma, aes(grup, As)) + geom_col() # Oluşturduğumuz grup değişkeni ile kalitelerine(arsenik etkisine) göre grafiğimizi oluşturalım

Suların kalitesine göre sınıflandırma yapılmıştır. Az Riskli, Orta Riskli ve Çok Riskli olarak gruplandırılabilir.
Grupların dağılımı;
knn_siniflandirma %>% group_by(grup) %>% summarise(Akarsu_Sayısı=n())
## # A tibble: 3 x 2 ## grup Akarsu_Sayısı ## <int> <int> ## 1 1 44 ## 2 2 2 ## 3 3 7
Bu çıktı ile veri setinde bulunda havza(akarsu) sayısının hangi gruplara girdiğini görebilmekteyiz.
Grupların illere göre dağılımı
knn_siniflandirma$IL[which(knn_siniflandirma$IL %in% c("Izmir/Selcuk","Izmir/Beydag","Izmir/Tire", "Izmir"))] <- "İzmir"
table(knn_siniflandirma$IL, knn_siniflandirma$grup)## 1 2 3 ## Balikesir 8 0 0 ## Bursa 7 0 0 ## Edirne 3 0 0 ## İzmir 11 1 1 ## Kirklareli 2 0 2 ## Kutahya 2 0 0 ## Manisa 9 1 0 ## Tekirdag 2 0 4 ## Usak 0 0 0
Sülfat, Toplam Çözülmüş Madde, Toplam Fosfor aralarındaki ilişki;
scatterplotMatrix(~SO4+TÇM+TP, regLine=FALSE, smooth=FALSE, diagonal=list(method="density"), data=ornekdata)

Tüm bu grafikler ve çıktılar incelendiğinde suların kalitelerine ve içeriklerine göre bir sınıflandırma yapabilmek mümkündür fakat yazının temel amacı keşifçi veri analizlerinden bazıları ile örnek çalışma yapmaktır.
Keşifçi veri analizleri sonucunda oluşturduğumuz gruplar incelendiğinde arıtma tesislerinin önemi görülmektedir. Fabrikaların atıkları sulara boşaltıldığında suyun içeriğini, sıcaklığını ve pH düzeylerini ciddi ölçüde etkilemektedir. Bu sebeple akarsu havzalarında yapılan fabrikalara arıtma tesisi kurulması gerekmektedir ve bunun belli bir standardı olmalıdır.
Bu yazımda veri bilimciler olarak bizler, sadece elimizdeki veriden makine öğrenimi algoritmalarını, derin öğrenme algoritmalarını gerçekleştirmekten ya da sadece veriyi modellemekten sorumlu değiliz. Yaptığımız Keşifçi Veri Analizleri ve İstatistik Bilimi ile mevcut olan sorunların belirlenmesi ve çözüm süreçleri konusunda da sorumluluk hissetmeliyiz.
Bu yazımda kısa bir keşifçi veri analizi ile Türkiye’de bulunan bazı akarsuların bileşenlerini inceleyerek mevcut sorunların analizini gerçekleştirdim. Bu yazımın asıl amacı; keşifçi veri analizi yöntemlerinin önemini vurgulamak, veriden neler ve ne gibi sonuçlar/yorumlar yapabilineceğini göstermektir. Keşifçi veri analizi, yaptığımız projelerde büyük önem taşımaktadır. Bu sebeple, neden-sonuç ilişkisini iyi kurmak, nedenselliği bilerlemek, sorunların neden kaynaklandığını(Pareto İlkesi bu konuda önemlidir) bilmek önem arz etmektedir.
Veri Çağında olduğumuzu unutmamalıyız. Veri okur yazarlığının önemini her yazımda vurguluyorum. Bu yazımda da verinin bize söylediği bilgileri anlamanın önemini belirterek sonlandırmak isterim. Keşifçi veri analizi(Exploratory Data Analysis(EDA)) ile neler yapabileceğimizi bir örnek veri seti ile önemine değinmiş olduk.
Saygılarımla.
Varsayımlarınızın sağlanması dileğiyle,
Veri ile kalın, Hoşça kalın..
Görsel Kaynak: http://amazinguniverse.net
Related Posts:
- Julius AI ile Veri Madenciliği ve Analizi
- Veri Kalitesi ve Yapay Zeka: Veri Mühendisliğinin Önemi
- Veri Madencilerinin Yeni Süper Gücü: Apify ile Kod…
- Veri Sürüm Kontrolü: Yazılımdan Veri Dünyasına
- Active Learning ve Veri Etiketlemedeki Rolü -Bölüm 1/2
- Debezium ile MySQL veri tabanı değişikliklerinin yakalanması