İstihdam Oranının Modellenmesinde Zaman Serisi Modellerinin Kullanımı

Gözde BOZKURT 4 Nisan 2019 Genel bir bakış, Zaman Serisi 2 2034 1605 kelime - 11 dakika52

---

Bu yazıya puan ver

(2 votes, average: 5,00 out of 5)

Loading...

---

Zaman serilerinin analizinin temelinde, serilerin özelliklerinin doğru şekilde belirlenmesi ve belirlenen özelliklere en uygun şekilde modelize edilmesi fikri yer almaktadır. Bu genel ifade de en önemli nokta “serilerin özelliklerinin doğru belirlenmesi”dir. Çünkü biliyoruz ki, “all models are wrong, but some are useful :)” (George E. P. Boz). Sadece bir zaman serisinin modelize edilmesi, bizi tek değişkenli model analizine götürmektedir. Tek değişkenli analiz teknikleri, finansal zaman serilerinde, hisse senetlerinde, döviz kurlarında vb. pek çok alanda faydalı ve kullanımı yaygınlaşmış tekniklerdir. Özellikler serilerin gelecekteki seyir davranışının belirlenmesi, bu alanla ilgili olanlar tarafından çok önemli bir noktadır. Bu nedenle bu yazımızda, “bir zaman serisinin özellikleri nasıl incelenmelidir?” sorusunun cevabını, tek değişkenli analiz tekniği kapsamında inceleyeceğiz.

Hadi o zaman 05.2006-11.2018 tarihleri kapsamında EVDS üzerinden temin ettiğimiz, İstihdam Oranı serisi için Eviews yardımıyla inceleyeceğimiz analizimize başlayalım. Öncelikle serinin seyrini bir görelim. Yapacağımız işlemlerde öncelikle Eviews üzerinden işlemin nasıl gerçekleştirildiğini, sonrasında da elde edilen çıktıyı inceleyelim.

Öncelikle yeni çalışma dosyası oluşturuyorum.

Sonrasında kullandığım veri setinin frekansı “aylık” olduğundan bunu belirtmem gerekiyor.

Aylık veri için incelediğim tarih aralığını belirtmem gerekiyor. Sonrasında serimi rahatlıkla Eviews’a aktarabiliyorum.

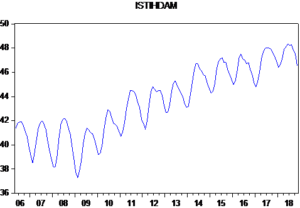
İstihdam oranı serisinin zamana bağlı olarak seyrinin arttığını gördüğümüzden, ortalamada durağan olmaması nedeniyle uzun dönem eğiliminin yani trendinin olduğunu söyleyebiliyoruz. Aynı zamanda dönemler arasındaki değerlerinin de değişmesi nedeniyle varyansta durağan olmadığını da söyeleyebiliriz. Bu arada düzenli dalgalanmalar nedeniyle “seri mevsimsel özellik mi barındırıyor acaba?” sorusu da geliyor aklıma. En iyisi otokorelasyon durumunu incelemek için bir de serinin korelogramına bakalım. İncelediğim serinin değerleri arasında “komşuluk bağı var mı?” buna bakayım.

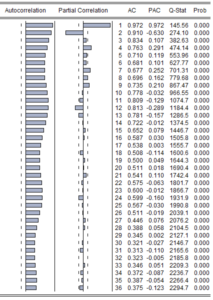
Otokorelasyon gecikmelerinin ortada kesikli olarak yer alan bandın dışında yer aldığını gördüğümden, seride otokorelasyon sorunu olduğunu düşünüyorum. Demek ki komşular arasında bir bağlılık var. Ayrıca gecikme dönemlerinde de yine bir dalgalanma var. O zaman, hem varyansta durağanlığı hem de eğrisel trendi doğrusal hale getirmemizi sağlayan logaritmiş dönüşümden yardım alıp tekrar bakalım. Bunun için de komut penceresini kullanalım.

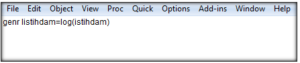
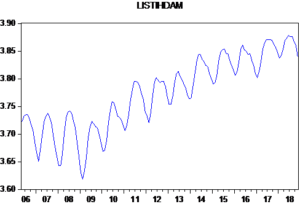
Logaritmik dönüşüm uyguladığım serinin ölçeğinin küçüldüğünü gördüm. Fakat diğer özelliklerin de hala incelenmesi gerektiğini düşünüyorum. Çünkü bilindiği üzere, işgücü istatistiklerinin olduğu seriler mevsimsel özellikler barındırmaktadır. Bu özellikler benim serimin durağan olması özelliğini engelliyor. Bu özelliği sağlayamazsam yanıltıcı sonuçlar elde ederim. Çünkü varyansta ve ortalama da görüyorum ki, sistematik bir değişim söz konusu olduğundan yapısal ilişkinin zaman içerisindeki değişimini kontrol edemeyeceğim. Fakat mevsimsel özellik taşıyan seriler için Dickey Fuller gibi testler yapmak doğru olmayacak. O zaman ben en iyisi Box-Jenkins yaklaşımı kullanayım. Yukarıda zaten serinin durağan olma özelliklerinin sağlanmadığını gördüm. Logaritmik dönüşüm yapmama rağmen mevsim bileşenlerinin zaman içerisinde sabitlenmediğini fark ettim. O zaman serinin durağanlığının sağlanması için bana bu yaklaşımın söylediği, serinin farkını alma işlemini gerçekleştireyim.

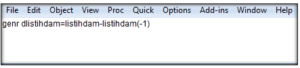
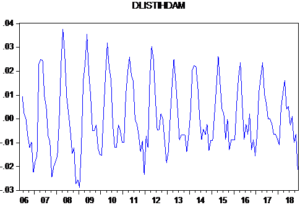
Serinin farkını alınca ortalamada durağanlığı sağladım. Bunu sağlasam da hala mevsimsellik durumunu çözemedim. O zaman farkı alınmış serinin bir de mevsimsel farkını alıp bakayım. Ama bu işlemi yaparken de, incelediğim serinin frekansının aylık olması nedeniyle, 12 döneme göre fark almam gerektiğine dikkat edeyim.

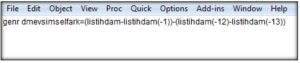
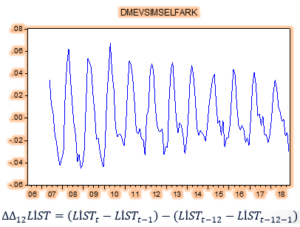
İlk farkını aldığım serinin mevsimsel farkını alınca da mevsim etkisinin hala olduğunu görüyorum. Ben en iyisi bir daha detaylı olarak serinin korelogramına bakayım.

Seride ki mevsimsellik 12 ve katlarında var. Yani bu seri aylık olduğu için, 12. 24. Ve 36. dönemlerde mevsimsellik olması, serimin bana “bende toplamsal mevsimsellik var!” demesi anlamına gelmedi. Yani örneğin, 11. ve 23. Dönemlerde mevsimsel bir bağ yok. Aylık seriyi ifade eden dönemlerde mevsimsellik var. O yüzden çarpımsal değil toplamsal mevsimsellik olduğunu, fark alma işlemlerinden sonra serim bana zaten söyledi. Ama şimdi de “ben serinin en uygun şekilde nasıl modelize edileceğine karar vereceğim?” sorusuna yanıt vermem lazım. Aklıma serilerin tüm özelliklerini barındırarak uygun formun belirlenmesi konusunda ve bu özellikleri sayesinde de öngörü performansının çok başarılı olduğu ARMA modelleri geliyor. Bu modeller yardımıyla serimi inceleyeyim diyorum. Ama burada şuna dikkat etmem gerekiyor. Seri durağan özelliklerde olmadığından ARMA değil de ARIMA modeli kullanmalıyım. Ama bir de mevsimsellik özelliğim var. En iyisi hepsini içinde barındıran SARIMA modeli kullanayım. Serimin özelliklerini her aşamada kontrol edip onu tanıdım. O yüzden en uygun olabilecek modelin belirlenmesinde, mevsimsel otoregresif model olan SARIMA bana tahmin için yardımcı olsun.

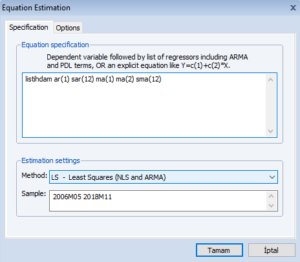
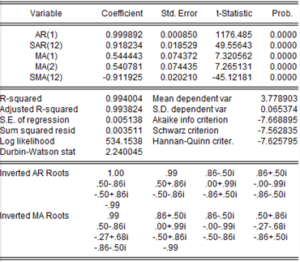
Serimin düzey hali ile aday modeli belirlemeye çalıştım. Çünkü zaten serimin özelliklerini modelize edebilecek en uygun aday modeli bulmaya çalışıyorum. Nasıl bir insanın özelliklerini değiştirmeye çalıştığımız zaman, mutsuz edici sonuçlar elde edebilme ihtimalimiz yüksekse, serim de bana aynı şeyi söylüyor. “Benim özelliklerimi yok etmeden beni modelize et, ben sana en uygun formu söyleyeceğim zaten” diyor. Serinin frekansı aylık olduğundan ve korelogramından da gördüğüm için, 12., 24. ve 36. dönemler için mevsimsel hareketli ortalama süreci (SMA) ve mevsimsel otoregresif süreç (SAR) deniyorum. Mümkün bütün kombinasyonları denedim ve yukarıda ki modelin aday model olduğunu düşündüm. Çünkü katsayılarım istatistiksel olarak anlamlı çıktı. E bir de otoregresif süreci temsil eden AR katsayısı 1’den küçük olduğu için durağanlık koşulunu sağladım. Ayrıca hareketli ortalama süreci olan MA(1) ve MA(2) katsayılarının toplamının 1’den küçük olması ile çevrilebilirlik koşulunu da sağladım. Ama “oh bitti en uygun model bu” demiyorum! Klasik ekonometrik varsayımların da sağlanması lazım. Yani bu aslında “bu zamana kadar beni yanıltmadı ama ben emin olmak için yine de onu bir deneyeyim” demekten başka bir şey değil. O zaman hadi deneyelim.

Serinin artık komşuluk bağı kalmadığını gördüm. Bulduğum aday model beni gecikmeli değerleri arasında ilişki olmadığını ispat ederek, otokorelasyon sorunu kalmadığına ikna etti. O zaman bir deneme daha yapayım.

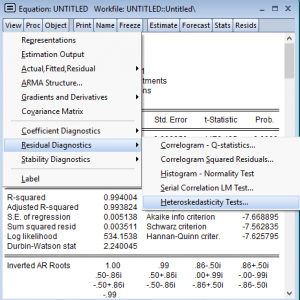
Aday modelim bana “varyansımda da değişim yok, sabitim, sürekli değişerek sana sorun yaratmayacağım” diyerek problemsiz olduğunu da gösterdi. Dur bakayım ben yine de bunlar ne kadar normal?

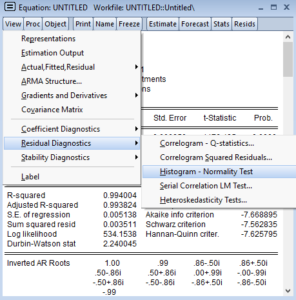
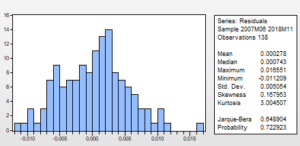
Tahmin ettiğim aday modelim bana “artıklarım da normal dağılmaktadır” diyerek güven verdi. Peki bu noktaya kadar modelim beni yanıltmadı ama ben bir bakayım serimi gerçekten ne kadar iyi temsil etti?

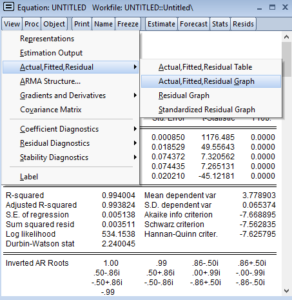
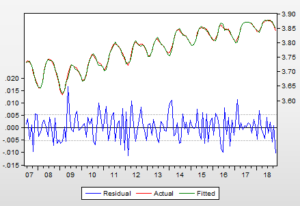
Tahmin edilen değerlerle gerçek değerlerin birbirini çok güzel temsil ettiğini görüyorum. Yani bulduğum aday modelin sözleri ile davranışları arasında tutarlılık olduğunu gördüm. Ama tabi ben güven sorunu yaşadığım için, bir de Box-Jenkins yaklaşımı beni etkilediği için “ayırt edici kontrol” yapayım.

Aday modelimin artıklarının korelogramına baktığımda, otokorelasyon olmadığı için “yanlış tanımlama yoktur” diyebiliyorum. Modelime artık güvenebilirim, beni şaşırtmadı. O zaman bir de öngörü yapayım da sonuçları bir genel olarak göreyim.

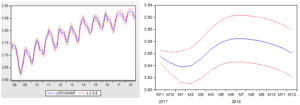
Sol tarafta 2008M05-2018M11 tarih aralığı için statik, sağ tarafta ise 2006M05 – 2017M11 tarih aralığı için tüm model tahmin edildikten sonra, 2007M11-2018M12 aralığına göre dinamik öngörü yaptım. Fakat öngörü kriterlerim değerlerini nasıl elde etmişim onlara bakayım.

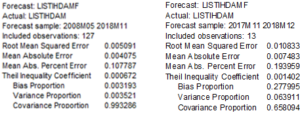
Karşılaştırma yapabileceğim başka bir model olmadığında, MAPE kriterine bakmakta fayda var. 0.19 ile bana iyi bir tahmin edici model olduğunu ispatladı. Ayrıca 0.06 varyans oranıyla da “ben değişkenlik gösterip, seni üzmem” de dedi. E sapma oranıyla da bunu gösterdi. Sapma ile varyans konusunda da dengeli olduğunu gösterdi. Hem dengeli, hem yanıltmayan, hem de öngörümüzü güzel yapan bir aday modeli ben artık incelediğim seri için “uygun model budur” diye belirlerim. “All models are wrong” derim ama, aynı zaman da bu model için, “but some are useful” da der ve haklı mutluluğumla yoluma devam ederim.

(Not.1: Yapılan çalışmalarda, belirlenen modeller için sadece RMSE (Root Mean Square Error) kriterine ait değeri verip iyi model diyebiliyorlar. Diğer kriterleri görmeden inanmayın derim:))

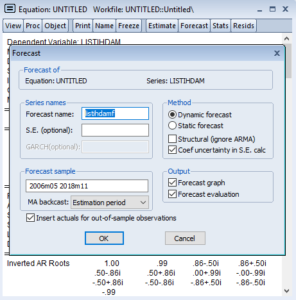
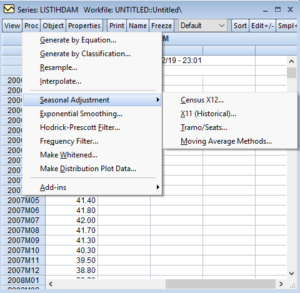
(Not.2: Eviews’ta uygun modelin belirlenmesi için aşağıda görseli verilen menü seçeneğinden de ilerleyebilirim. Ama her zaman en uygun modelin belirlenmesinde, mümkün tüm kombinasyonların bizim tarafımızdan denenmesi ve kontrol edilmesi benim tercihimdir:))