Bootstrap (Yeniden Örnekleme) Nedir ?

Utku Kubilay ÇINAR 21 Mayıs 2019 Yeni Başlayanlar 0 13376 934 kelime - 6 dakika138

Bu yazıya puan ver

(1 votes, average: 3,00 out of 5)

Utku Kubilay ÇINAR

Bootstrap Yöntemi, istatistik alan(lar)ında sıklıkla kullanılan yöntemlerin başında gelmektedir. Bootstrap yöntemleri ya da algoritmalarındaki asıl amaç veriden, büyük veri setleri oluşturmak (üretmek) ve yeniden örnekleme yapmaktır.

Bootstrap yönteminde, yapılacak olan yorumu bazı parametrelerin istatistiksel çıkarımlarıyla yeniden çizilmesiyle yapılmaktadır. Ardından bu işlemin daha güvenilir olabilmesi için fazlaca tekrarlanır. Bootstrap yöntemiyle, varyans tahminleri başarılıyla elde edilmektedir ve varyans tahminleri konusunda sıklıkla kullanılmaktadır. Ayrıca Bootstrap metodu, örnek dağılışının normal olmadığı durumlarda ya da çok küçük veri setlerinde varyans analizine göre üstünlük taşımaktadır (TAKMA, Ç. ve ATIL, H).

Bootstrap metodu, yoğun matematik formüllerinden uzak, sınırlı varsayımlara sahip, anlaşılması ve kullanılması oldukça kolay bir yöntemdir (Simon ve Bruce, 1991). Özellikle varsayımların yetersiz kaldığı durumlarda güvenilir sonuçlar vermektedir. Bootstrap metodu, olasılıkta olduğu gibi (Takma, Ç. ve Atıl, H.), güven aralıkları, hipotez testi ve regresyon analizinde de kullanılmaktadır (Efron ve Tibshirani 1993).

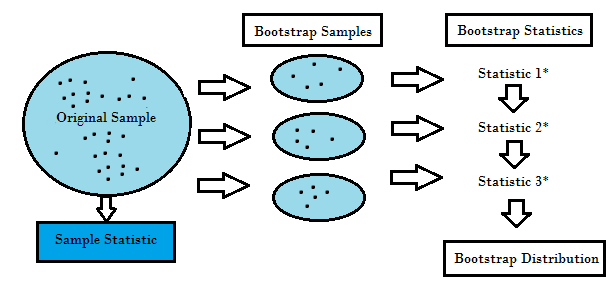
Bootstrap Örneklemesi

Kitle dağılımı hakkında hiçbir varsayım yapılmamışsa, küçük hacimli örneklemede, kitle ortalaması için güven aralığı söyleyemeyiz, aralık tahmini yapamayız. Bu gibi sorunların altından kalmak için elimizdeki veri üzerinde “yeniden n hacimlik örneklemeler” yapılıp, ilgili istatistiğin değeri çok kez gözlenip, dağılımı hakkında fikir elde edilebilir. (Kaynak: http://80.251.40.59/science.ankara.edu.tr/ozturk/Dersler/ist312/Ders10/Ders10.pdf)

Uygulama

R programındaki hazır veri seti üzerinden Bootstrap örneklemesi kullanarak yeni gözlemler oluşturalım. “ACSWR” kütüphanesinden “nerve” veri seti bu analizde kullanılmıştır.

library(ACSWR) # veri seti için
data("nerve")
library(boot) # Bootstrap İşlemleri için Kullanılan Kütüphane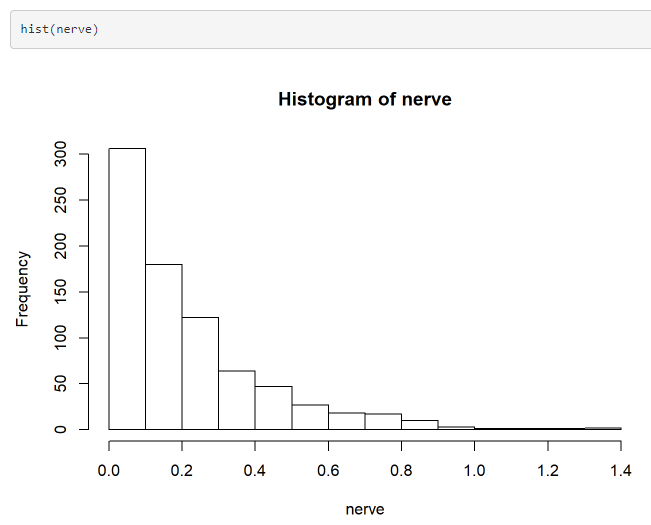

carpiklik <- function(x,i){

ort = mean(x[i]) 
toplam = sum((x[i]-ort) ̂ 2)/length(x[i])
ortalama = mean((x[i]-ort) ̂ 3)/(toplam ̂ (3/2)) 
return(ortalama) 
}

# örneklemenin temsiliyet durumu

# 1.000 örneklem ile işlemimizi yapalım

boot(data = nerve, # veri seti
     statistic = carpiklik , # yapılacak işlem
     R =c1000) # Bootstrap işlemi tekrar sayısı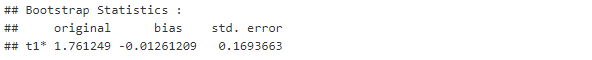

Yaptığımız işlemler sonucunda orjinal değerimiz 1.76 olarak bulunmuştur. Yaklaşık 1.000 tane bootstrap yani yeniden örnekleme yaptığımızda orjinal veriye olan yanlılığımız (bias) 0.012 olmuştur, standart sapmamız ise 0.16 olarak belirlenmiştir. Dağılımını bilmediğimiz bir veriden üretilen yeni örneklemlerin yanlılık ve sapma değerleridir.

Eğer 1.000 tekrar yerine 5.000 tekrar yapsaydık yani, bootstrap değerimizi (R) yükselttiğimizde yanlılık ve sapma değerimiz nasıl bir değişime uğrayacak bunu inceleyelim.

# 5.000 örneklem ile

boot(data = nerve, # veri seti
     statistic = carpiklik, # yapılacak işlem
     R = 5000) # Bootstrap işlemi tekrar sayısı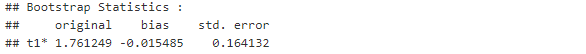

Görüldüğü üzere yanlılık hafif miktarda artmış ve standart sapmamız azalmıştır.

Başka bir Uygulama Yapalım

İris veri seti ile yeniden örnekleme yapalım ve ürettiğimiz veriler ile orjinal verilerin yanlılığını-sapmalarını inceleyelim.

# istatistik fonksiyonu oluşturalım. Bununla 2 bileşenli veri setimizde bileşenler arasındaki ilişkiye bakalım ve ayrı ayrı ortanca değerlerini inceleyelim.

istatistik <- function(data, indeks){

  dt= data[indeks,]

  c(
    cor(dt[,1], dt[,2], method = "s"), # spearman korelasyonu
    median(dt[,1]),
    median(dt[,2])
    )
}

bootstrap_sonuc <- boot(data = iris, # iris veri seti
                    statistic = istatistik, # oluşturduğumuz fonksiyon
                    R=1000) # Bootstrap işleminde tekrarlı örnek sayısı (number of repetitions)
                   
# $t0 = Orjinal veri
# $t = ürettiğimiz veri

# bootstrap_sonuc$t = bootstrap prosedürü (R'nin bootstrap gerçekleştirmeleri) tarafından oluşturulan istatistiklerimizin R değerlerini içerir.

head(bootstrap_sonuc$t, 10)

##              [,1] [,2] [,3]
##  [1,] -0.26405188 5.70  3.0
##  [2,] -0.12973299 5.80  3.0
##  [3,] -0.07972066 5.75  3.0
##  [4,] -0.16122705 6.00  3.0
##  [5,] -0.20664808 6.00  3.0
##  [6,] -0.12221170 5.80  3.0
##  [7,] -0.29356913 5.70  3.0
##  [8,] -0.11368900 5.70  3.0
##  [9,] -0.15260835 5.85  3.1
## [10,] -0.15772740 6.00  3.0

bootstrap_sonuc$t0 # Orjinal veri setindeki istatistiklerimiz ( korelasyon, medyan 1, medyan 2)

## [1] -0.1667777  5.8000000  3.0000000

bootstrap_sonuc # Parametrik Olmayan Bootstrap işlemimizdeki sapma ve yanlılık değerlerimiz 
# (gerçekleşen ile ürettiğimiz arasındaki fark (korelasyon - medyan 1 - medyan 2 değerleri farklılıkları))

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = iris, statistic = istatistik, R = 1000)
## 
## 
## Bootstrap Statistics :
##       original       bias    std. error
## t1* -0.1667777  0.002546391  0.07573983 # korelasyon 
## t2*  5.8000000 -0.013350000  0.10295571 # medyan 1 
## t3*  3.0000000  0.007900000  0.02726414 # medyan 2

Orjinal veriye göre ürettiğimiz değerlerin sapmaları ve yanlılıkları tablodaki gibidir.

Güven Aralıklarını İnceleyelim

Nokta tahmini yapmaktansa Güven Aralıkları ile yapılan tahminler daha fazla bilgi vermektedir. Bu sebeple Bootstrap yönteminde hipotez testleri ve güven aralıklarının kullanılmasındaki asıl amaç, veri setimizin dağılımını bilmeden hipotez testinin yapılmasıdır.

boot.ci(bootstrap_sonuc, index=1, type=c('basic','perc'))

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = bootstrap_sonuc, type = c("basic", "perc"), index = 1)
## 
## Intervals : 
## Level      Basic              Percentile     
## 95%   (-0.3212, -0.0329 )   (-0.3007, -0.0124 )  
## Calculations and Intervals on Original Scale

Olarak güven aralıklarını bulmuş oluyoruz.

Varsayımlarınızın sağlanması dileğiyle,

Veri ile kalın, Hoşça kalın..

Kaynakça

EFRON, B. and Tibshirani, R., (1993), An introduction to the Bootstrap, Chapman and Hall, New York.
TAKMA, Ç. ve ATIL, H., (2006), “Bootstrap Metodu ve Uygulanışı Üzerine Bir Çalışma 2. Güven Aralıkları, Hipotez Testi ve Regresyon Analizinde Bootstrap Metodu”, Ege Üniversitesi, Ziraat Fakültesi Dergisi, 43(2):63-72.
WEHRENS, R., H. Putter and L.M.C. Buydens, (2000), The bootstrap: a tutorial. Chemometrics and Intelligent Laboratory Systems, 54:35-52.
https://www.datacamp.com/community/tutorials/bootstrap-r
Görsel Kaynak: https://www.statisticshowto.datasciencecentral.com/bootstrap-sample/