
![]()
Derlenen veri üzerinde herhangi bir işlem yapılmamışsa bunlara ham veri ya da sınıflandırılmamış (gruplandırılmamış) veri denir.
- Birim sayısı az olan yığınların çeşitli özellikleri ham veriye dayanarak kolaylıkla belirtilir.
- Yığın çok sayıda birimden oluşuyorsa, bunları sınıflandırmakla yığının çeşitli özelliklerini belirlemek kolaylaşacaktır.
Sınıflandırmanın en doğru yolu frekans tablosudur. Burada, gözlenen veri sınıflara ayrılır. Sonuçlanan tablo her bir sınıftaki gözlem sayısını verecektir.
Relatif Frekans: Bir deney n kez yapıldığında bir A olayı f kez gerçekleşirse, f/n oranına A olayının relatif frekansı denir. n artarken f/n relatif frekansının bir limite yaklaştığı kabul edilirse, bu limite A’nın olasılığı denir. Uygulamada büyük n ler için A’nın olasılığı f/n ile hesaplanır. Bilinen nedenlerle olasılığın frekans tanımı denir.

Frekans tablosunu hazırlamak için aşağıdaki adımlar izlenir.
1.Adım: Gözlemlerin sayısı belirlerin. n = Gözlem sayısını gösterir (50 ≤ n tercih edilir).
2.Adım: En büyük değer (maksimum) ve en küçük değer (minimum) bulunur. Aradaki fark hesaplandığında ise değişim aralığı (range) elde edilir.
3.Adım: Sınıf sayısı bulunur.

Kesin bir yaklaşım olmamakla birlikte sınıf sayısı için k = 1 + 3.3 * log(n) formülü de kullanılabilir. Genel olarak 5 ≤ k ≤ 20 seçilmesi beklenir.
4.Adım: Sınıf genişliği Ardışık iki sınıfın alt ya da üst sınıf limitleri arasındaki farka dağılım için sınıf genişliği denir. Başka bir sınıflamaya gerek duyulmadıkça sınıf genişliklerini eşit alınır.
Sınıf genişliği = h ’dır. Range = R ’dir. Sınıf sayısı = k ’dır.

5.Adım: Sınıf limitleri, frekans dağılımında sınıfları belirlemek için kullanılan sayılardır. En küçük gözlem değerine eşit ya da daha küçük olarak ilk sınıfın alt limiti seçilir. Bu değere ardışık olarak sınıf genişliğinin eklenmesiyle diğer sınıfların alt limitleri bulunur. Verinin sürekli ya da kesikli olmasına göre ilk sınıftan başlayarak üst limitler de aynı yolla bulunur.
6.Adım: Sınıf sınırları belirlenir.

[i. sınıfın üst sınıf sınırı = (i+1). sınıfın alt sınıf sınırıdır]. Sınıf sınırları arasındaki (üst sınır – alt sınır) fark bir sınıfın sınıf genişliğini verir.
7.Adım: Sınıf frekansı, her bir sınıf için -sınıf limitleri dahil -o sınıfa düşen gözlem sayısı (sınıf frekansı) saptanır.
8.Adım: Sınıf orta noktası, sınıf limitlerinin ya da sınıf sınırlarının ortalaması alınarak her sınıf için sınıf orta noktaları bulunur.
9.Adım: Frekanslar toplanarak kontrol edilir.
10.Adım: Kümülatif frekans, ardışık olarak frekanslar toplanarak kümülatif (eklemeli) frekans sütunu oluşturulur.
UYGULAMA
Uygulama verisine aşağıdaki linkten ulaşabilirsiniz.
http://courses.wccnet.edu/~palay/math160r/r_groups.htm

1.Aşama: Gözlem sayısı
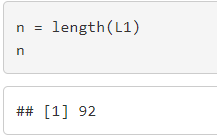
2.Aşama: Değişim Aralığı (Range)
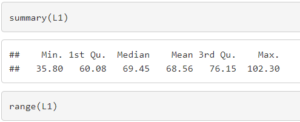
Range değerleri 35.8 ve 102.3’tür. En küçük ve en büyük değer olarak 30 e 110 sayılarını kullanabiliriz.
3.Aşama: Sınıf sayısı, k = tamsayı

Sınıf sayısı 9.59 yerine en büyük ve yakın tam sayı olarak 10 alınsın.
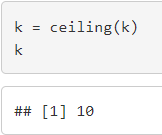
4.Aşama: Sınıf genişliği
(Değişim Aralığı / Sınıf Sayısı) = h yani (range / k) = h max = 110, min = 30, k = 10
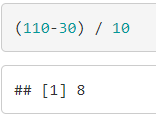
8 sınıf oluşacaktır.
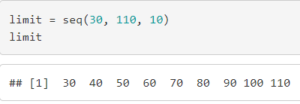
5.Aşama: Sınıf Limitleri
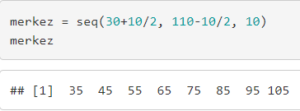
8.Aşama: Sınıf orta noktası – Sınıf merkezi
Veriyle sınıfların oluşturulması

7.Aşama Gruplandırılmış verinin frekansı

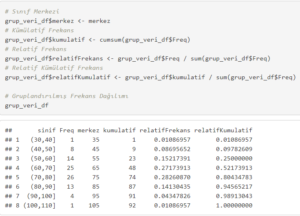
Gruplandırılmış Veri ve Frekanslar

Gruplandırılmış (Sınıflandırılmış) veriye sınıfın merkezi, kümülatif artan frekansı, relatif frekansı ve kümülatif relatif frekansı ekleyiniz.
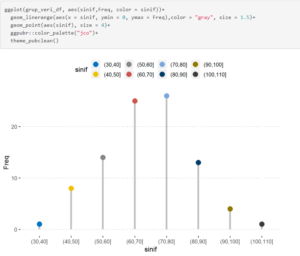
Çizgisel Grafik
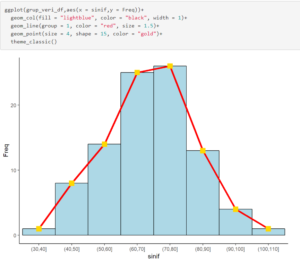
Histogram ve Frekans Poligonu
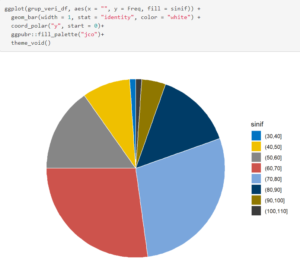
Dairesel (Pie) Grafik
Kümülatif Frekans Dağılımı

Bir sonraki yazılarda görüşmek üzere.
Kaynak: Fikri Akdeniz – Olasılık ve İstatistik
Veri: http://courses.wccnet.edu/~palay/math160r/gnrnd4.R