Kategorik Veri Analizi ve Shiny Web Uygulamaları – 4
(No Ratings Yet)
Loading...Günümüzde gelişen teknolojilerle birlikte elimizdeki verileri kullanarak matematiksel modeller oluşturup, araştırılan konular hakkında tahminlemeler yapabiliyoruz. Bunu istatistik ile, yani belirli bir hata payı ile yapıyoruz. Örneğin bir bölgenin gelir seviyesinin incelendiği bir çalışmayı ele alalım ve bu çalışmada Doğrusal Regresyondan yararlandığımızı düşünelim. Doğrusal Regresyon, hata kareler toplamını en küçüklemeyi amaçlayan bir yöntemdir.
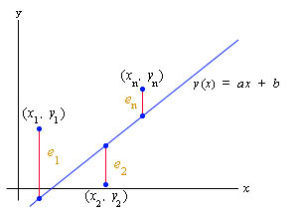
Şekilde belirtilen noktalar, her bir gözlenen değeri temsil ediyor. Bu değerlere en yakından geçebilecek, yani en az hata ile geçebilecek doğruya ise regresyon doğrusu deniyor.
“Hata” olarak bilinen 
değeri her bir gözlenen değer için; 
şeklinde hesaplanır. Her bir gözlenen değerden, doğru üzerinde tahmin edilen değeri çıkarttığımızda o değişkene ait hata değerini elde ediyoruz.
değeri model tarafından açıklanamayan kısım olarak bilinir. Yani doğal sebeplerden dolayı oluşan değişkenliklerdir ve herhangi bir matematiksel altyapısı bulunamaz.
Peki doğal nedenlerden dolayı oluşan hataları nasıl minimize edebiliriz? Nasıl daha kesin tahminler yapabilen modeller geliştirebiliriz? Model kurma mantığı temel anlamda tüm örnekleri yakalayabilme, doğru tahminler yapabilme üzerine kurulmaktadır. Sonuç olarak, hataların azaltılması gerekiyor ve bu hatayı insan doğasına, yaptıkları seçimlerin özgürlüğüne müdahale etmeden azaltmak mümkün değil.
Aldous Huxley, 1984 kitabında işlenen distopya kavramını, 26. yüzyılda gerçekleşen, insanlara ait değerlerin yok edildiği, sanatın, edebiyatın, dinin tamamen ortadan kaldırıldığı bir dünya düzeni şeklinde anlatır. Yapay döllenme ile üretilen yumurtalara “bokanovski işlemi” olarak adlandırılan bir işlem uygulayarak döllenmiş yumurtanın normal büyümesini engelleyip, yumurtanın tomurcuklanması sağlanır. Tek bir yumurtadan 96 tane eş(ikiz) elde edilir. Bu ikizler toplumsal düzenin alfalarını, betalarını, gammalarını, deltalarını ve epsilonlarını oluştururlar.
Sosyal sınıfları belirleme süreci yumurtalar şişelerin içlerine doldurulduktan sonra başlar. Çeşitli kimyasallarla doğacak olan grubun alfa mı, beta mı yoksa epsilon mu olacağına önceden karar verilir ve süreç başlatılır. Doğduklarında kaderleri belli olan çocuklar “şartlandırma odaları” adı verilen bölümlerde, bulundukları sosyal sınıfa ait çeşitli şartlandırmalara maruz kalırlar. Bireylere kendi sınıflarına ait olmalarının ne kadar büyük bir şans olduğu öğretilir ve hiçbir zaman başka bir sosyal sınıfa ait olma isteği duymamaları için çok derin dürtülere sahip olmaları sağlanır.
“Çelik olmadan araba yaratamazsınız – aynı şekilde, sosyal çalkantı olmadan da trajedi yaratamazsınız. Dünya şu anda istikrara kavuşmuş durumda. İnsanlar mutlu; istediklerini alıyorlar ve ulaşamayacakları şeyleri de asla istemiyorlar. Refahları yerinde; emniyetteler; hiç hastalanmıyorlar; ölümden korkmuyorlar; ihtiras ve ihtiyarlıktan habersiz ve bundan da çok memnunlar; veba gibi bir illet olan anne ve babaları yok; güçlü duygular hissedecekleri eşleri, çocukları ve sevgilileri yok; şartlandırmaları uyarınca davranmaları gerektiği gibi davranmak zorundalar. Herhangi bir sorun çıkması durumunda da soma var. Siz de tutup, özgürlük adına pencereden savurdunuz, Bay Vahşi. Özgürlük!”(Huxley, Cesur Yeni Dünya)
Böyle bir dünya düzeninin sağlanmasındaki motivasyon ne olabilir? Bireylerin belirli bir düzen içerisinde, tahmin edilebilir rollerde yaşaması kimlerin işine yarayabilir?
Sonuç olarak, değişkenliklerin azaltılması ve sapmaların engellenmesi, kurulan regresyon modellerinin daha düşük hata ile tahmin etmesini sağlayabilir ancak ekranı başında varsayımları kontrol edip, analiz yapmaya başlayan bir öğrenci, aldığı sonuçlardan ne derece heyecan duyar? Yapay bir dünyanın, öngörülebilir tahminleri… Aynı müziğin yokluğu gibi.
Lojistik Regresyon
Lojistik regresyon analizini R’da nasıl yapacağımızı öğrendik. Bu yazımda yaptığımız analizlerin yorumlanması üzerinde duracağım. Ek olarak, ideal modelin tercih edilmesi süreci hakkında bilgiler verdikten sonra Shiny’de uygulamasını yapacağım.
Odds Değeri :
Odds değeri bir durumun gerçekleşmesi ve gerçekleşmemesi arasındaki ilişkiyi gösterir. Bu değer olayın gerçekleşmesi olasılığının, gerçekleşmemesi olasılığına bölümüyle bulunur. Gerçekleşmesi olayına P dersek;
10 tane atın yarıştığı bir yarışı düşünelim. 5 numaralı atın birinci gelmesi odds’u şu şekilde hesaplanır;
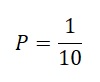
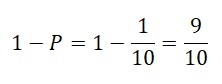
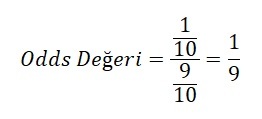
5 numaralı atın birinci gelmesi oddsu 1/9 olarak bulunur. Şans oyunlarında genelde bu istatistik kullanılır ve halk arasında 1’e 9 olarak da bilinir.
Odds Oranı :
Odds oranı iki adet Odds değerinin birbirine oranlanmasıyla oluşan bir ölçüm değeridir. Bu değeri hesaplarken araştırmak istediğimiz bilgiyi ve referans aldığımız noktayı doğru tespit etmeliyiz. Örneğin sigara içen insanların akciğer kanseri olması durumunu araştırıyorsak eğer, sigara içmeyen insanları referans almamız gerekiyor. Bunu bir formül ile göstermek gerekirse;
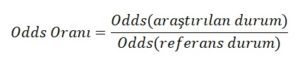şeklinde formüle edilir.
Örnek :
- Sigara içen kişilerde akciğer kanseri olma olasılığı 8/10 olsun. Bu durumda, sigara içen kişilerin akciğer kanseri olması odds’u 4 olur.
- Sigara içmeyen kişilerde akciğer kanseri olma olasılığı 4/10 olsun. Bu durumda, sigara içmeyen kişilerin akciğer kanseri olması odds’u 2/3 olur.
- Bu iki değeri oranladığımızda 4/(2/3) = 6 sonucunu elde ediyoruz.
## Sigara içen kişilerin akciğer kanseri olması odds’u, sigara içmeyen kişilerin akciğer kanseri olması odds’unun 6 katıdır.
Lojistik Regresyon’da Katsayıların Yorumlanması
Lojistik Regresyon’da katsayılar odds oranı kullanılarak yorumlanır. Odds değerini hesaplarken kullandığımız temel parametre başarı olasılığıdır, yani P değeridir. Lojistik regresyonda da hesapladığımız parametre aynı şekilde P değeridir. Lojistik regresyon ile hesapladığımız P değeri bize bir olayın gerçekleşmesi olasılığını söylüyor fakat bu olayı farklı yönleri ile değerlendirmek, iki veya daha fazla durumun birbiri ile olan ilişkisini ölçmek için Odds değeri vazgeçilmez bir istatistik oluyor.
Lojistik regresyonda;
Lojistik regresyon modeli 
Logit dönüşümü yapılmış lojistik regresyon modeli 
Bağımsız değişken olan X değişkeninin kesikli veya sürekli olması, Odds oranı hesaplamada bir farklılık göstermez;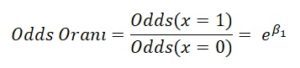
şeklinde hesaplanır. Sadece yorumlarken bağımsız değişkenin tipi önemlidir.
Örnek :
Bir kişinin sigara içmesi ile kanser olması arasındaki ilişkiyi ölçen bir çalışmada model
şeklinde kurulmuş olsun.
X : Kişinin sigara içip içmediği ( Evet : 1 – Hayır : 0)
Y : Kişinin kanser olup olmadığı ( Evet : 1 – Hayır : 0)
şeklinde hesaplanır.
- X değişkeni 2 düzeyli kategorik değişken. X değişkenini yorumlarken referans aldığımız noktaya göre yorum yapılır
## Sigara içen kişilerin kanser olma odds’u, sigara içmeyen kişilerin kanser olması odds’unun 9.025 katıdır.
- X değişkeni, kandaki nikotin miktarı gibi sürekli bir değişken olsaydı;
## Kandaki nikotin miktarındaki bir birimlik artış ile kişilerde akciğer kanseri görülmesi odds’u, şu anki nikotin miktarına göre kişilerde akciğer kanseri görülmesi odds’unun 9.025 katıdır.
– Ek olarak, burada odds değerini ve yorumunu 1 birimlik artışa göre hesaplıyoruz. Çalışmanızda 3 birim, 10 birim, 100 birimlik artışları incelemek istiyorsanız;
burada X değişkeninin 3 birim artışıyla hesaplanan odds oranını görüyoruz. Sonuçlar tam olarak gerçeği yansıtmasa da yorumlamaları genel olarak anladığınızı umuyorum 🙂
## Kandaki nikotin miktarındaki 3 birimlik artış ile kişilerde akciğer kanseri görümlesi odds’u, şu anki nikotin miktarına göre kişilerde akciğer kanseri görülmesi odds’unun 735.09 katıdır.
Yorumlarken her zaman bağımlı değişken olan Y değişkeninin başarı olasılığı ile ilgileniyoruz. Karşılaştırdığımız şey, bağımsız değişken olan X değişkeninin farklı düzeyleri.
Eğer bağımsız değişken olan X değişkeni kategorik ve 2’den fazla düzeye sahip ise;
- Kategorik değişkenler modele düzey sayısının 1 eksiği kadar “kukla” değişken olarak girer. Örneğin X değişkeni 4 düzeye sahip bir kategorik değişken ise (4-1) adet değişken modele girer.
- Kukla değişkenlerinin kodlaması iki şekilde yapılır; referans kodlama ve ortalamadan sapma kodlama. R programında otomatik olarak yapılan kodlama şekli referans kodlamadır ve odds oranı(Q) tahmini;
şeklinde hesaplanır.
şeklinde hesaplanır.“Uygarlığın kahramanlık ya da yüceliğe hiç ihtiyacı yoktur. Bunlar, politik yetersizliğin belirtileridir. Bizimki gibi düzenli bir toplumda, hiç kimsenin kahraman ya da yüce olma fırsatı olmaz. Böylesi bir olgunun yaşanması için koşulların bütünüyle dengesiz olması gerekir. Savaşların yaşandığı, bölünmüş ittifakların olduğu yerlerde, baştan çıkmamak için mücadele verilen yerlerde, uğruna savaşılacak ya da savunulacak aşkların olduğu yerlerde yücelik ve kahramanlığın bir anlamı olabilir elbette. Fakat şimdi savaşlar yaşanmıyor. Birini çok fazla sevmemeniz için büyük bir özen gösteriliyor. Bölünmüş bir ittifak söz konusu bile olamaz; öylesine şartlandırılırsınız ki, sizden beklenenleri yapmamak elinizde değildir. Yapmanız beklenen şeyler genelde öyle keyiflidir ve öyle çok sayıda doğal dürtünüz özgürce tatmin edilir ki, baştan çıkmamak için mücadele edilecek hiçbir şey bulamazsınız.”(Huxley, Cesur Yeni Dünya)
Odds Oranı için Güven Aralığı
Bulduğumuz tahmin değeri odds oranının nokta tahminidir. İstatistikte her zaman bir nokta tahmini ve o tahminin bir güven aralığı vardır. Öncelikle bilmemiz gereken odds oranı değerinin örnekleme dağılımıdır. Odds oranının dağılımı çarpık bir dağılımdır, çünkü bu değer 0 ile +sonsuz arasında yer alır ve 1 noktasında etkisidir. Örneğin sigara içenlerin kanser olma odds’u ile içmeyenlerin kanser olma odds’u birbirine eşitse hiçbir fark yok demektir.
Bu nedenle 
katsayısının aralık kestiriminden yola çıkarak odds oranı için güven aralığı hesaplanır.
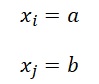
İdeal Modelin Tercih Edilmesi
Uygulamada kullanacağımız veri seti hakkında genel bilgiler;
Prostat kanseri tedavisinde kullanılan bir ilacın tedavi edici olup olmamasını etkileyen faktörler araştırılıyor.
Bağımlı Değişken;
- CAPSULE değişkeni : İlacın etki durumu(0: İlacın etkisi yok – 1: İlacın etkisi var)
Bağımsız Değişkenler;
- Age : Yaş
- Race : Irk (1:Beyaz, 2:Beyaz olmayan)
- DPROS : Hastadaki kanser nodülü(1:Nodül yok – 2:Sağ nodül – 3:Sol nodül – 4:Çift loblu nodül)
- DCAPS : Rektal uygulamada kapsülün etki etmesi(1:Hayır – 2:Evet)
- PSA : Tümör volümünden elde edilmiş antijen değeri(Mg/ml)
- VOL : Ultrasonda elde edilen tümör hacmi
- GLEASON : Toplam gleason skoru(0-10)
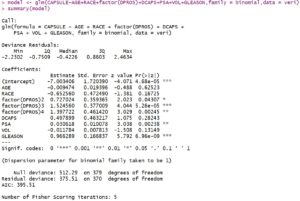
1- Modelin anlamlı olup olmadığının test edilmesi; bağımlı değişken üzerinde etkisi olduğunu düşündüğümüz tüm değişkenlerle bir model oluşturduk. Şimdi bu değişkenlerden en az bir tanesinin anlamlı olup olmadığını test edeceğiz.
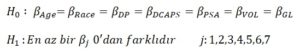
Lojistik Regresyonda, model anlamlılık testlerinde G test istatistiği kullanılır.
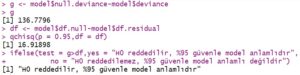
Model anlamlılığının test edilmesi ile ilgili aklınıza takılan herhangi bir şey olursa, “Kategorik Veri Analizi ve Shiny Web Uygulamaları – 2” yazısını inceleyebilirsiniz.
## H0 hipotezi reddedildi ve %95 güvenle modelin anlamlı olduğuna karar verildi. Yani kurduğumuz modeldeki değişkenlerden en az bir tanesi anlamlıdır sonucuna varıyoruz. Ancak hangi değişkenin veya değişkenlerin anlamlı olduğuna karar vermek için teker teker katsayıların anlamlılıklarını test etmemiz gerekiyor.
2- Katsayıların anlamlılıklarının test edilmesi; model anlamlılık testinde en az bir değişkenin anlamlı olduğunu belirledik. Tek tek anlamlılık testi yapmak yerine, model hakkında özet bilginin olduğu tabloya bakarak her bir değişkenin p değerinin alpha değerinden büyük olup olmadığına bakarak değişkenlerin anlamlı olup olmadığına karar verebiliriz.
Lojistik Regresyonda, değişkenlerin anlamlılıklarını test etmek için Wald test istatistiği kullanılır.
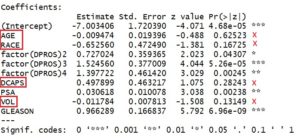
%95 güvenle AGE, RAGE, DCAPS ve VOL değişkenlerinin bu model için anlamlı olmadığını belirledik. Anlamsız olan değişkenleri direk olarak modelden çıkarmak doğru değildir. Herhangi bir bilgi kaybına sebebiyet vermemek için ilk önce anlamsız olduğunu belirlediğimiz değişkenler ile ilgili bir hipotez kurmamız gerekiyor.
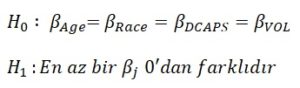
2.1- Yukarıda kurulan hipotezdeki H0 hipotezinin doğruluğu altında, anlamsız olduğu belirlenen değişkenleri çıkarıp anlamlı olan değişkenler ile bir model kuruyoruz. Ve bu model, bizim azaltılmış modelimiz oluyor.
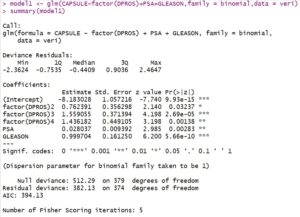
Azaltılmış modelin anlamlılığını kontrol etmek için G test istatistiğini kullanarak modelin anlamlılığını test ediyoruz. Model1 değişkenine atadığımız azaltılmış modele ait anlamlılık testi aşağıdaki gibidir.
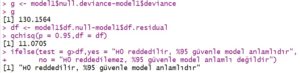
Azaltılmış model kendi içinde anlamlı olmalıdır.
Full modelin de azaltılmış modelin de anlamlı olduğunu kanıtladık. Hangi modeli tercih edeceğimize karar verirken, ilk bölümde anlamsız olan değişkenler ile kurduğumuz hipotezi test etmemiz gerekiyor. Modelden çıkarılması planlanan değişkenler;
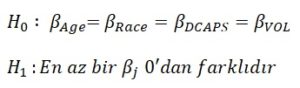
3- Uygun modelin tercih edilmesi;
Burada bizim asıl test ettiğimiz şey modelden çıkardığımız değişkenlerin anlamlı bir değişime sebep olup olmadığını bulmak. Şuan elimizde full modele ve azaltılmış modele ait bilgiler var. Bu iki modelin artık sapmaları(residual deviance) arasındaki fark çok büyük değilse, azaltılmış modeli tercih etmemiz mantıklı olacaktır. Çünkü çıkartılan değişkenlerin model açıklayıcılığı üzerinde çok büyük bir etkisi yoktur. Bu farkı bulabilmek için azaltılmış modelin residual deviance’ından, full modelin residual deviance’ını çıkarıyoruz.
H0 hipotezi %95 güvenle reddedilemedi. AGE, RACE,DCAPS,VOL değişkenlerinden en az birinin modele anlamlı katkısı olduğunu söyleyecek yeterli kanıt yoktur.Bu değişkenler modelden çıkartılabilir.
3.1- Özet tabloda, AIC değeri bulunuyor. Bu değer Akaike Bilgi Kriteri olarak adlandırılıyor ve bu istatistik iki model arasında seçim yapmak için kullanılır.
AIC değeri küçük olan model seçilir.
Full modelin AIC değeri : 395.5092
Azaltılmış modelin AIC değeri : 394.1324
Sonuç olarak AIC değerlerini karşılaştırarak da azaltılmış modeli tercih etmemiz gerektiğini görüyoruz.
“Istırap karşılığında kazanılan şeylerle kıyaslandığında, şu andaki mutluluk çok sefil kalır. Ve tabii ki istikrar, istikrarsızlık kadar gösterişli değildir. Mutlulukta, şanssızlığa karşı verilen mücadelenin ihtişamlarından hiçbiri yoktur. Günahla mücadelenin veya ihtiras ya da şüphe nedeniyle ölümüne altüst oluşların görkemini bulamazsınız mutlulukta. Mutluluğun yüce bir yanı yoktur.”(Huxley, Cesur Yeni Dünya)
Örnek :
- Tümör volümünden elde edilmiş antijen değerine(PSA) ait odds oranını tercih ettiğiniz modele göre yorumlayınız.
## Modeldeki diğer tüm değişkenler sabit iken, tümör volümünden elde edilmiş antijen değeri 1 mg daha fazla olan hastalarda ilacın etki etmesi oddsu, 1 mg’dan fazla olmayan hastalarda ilacın etki etmesi odds’unun 1.03 katıdır.
- Hastadaki kanser nodülü sol tarafta olan hastalara ait(DP3) odds oranını yorumlayınız.
## Modeldeki diğer tüm değişkenler sabit iken, sol nodülü olan hastalarda ilacın etkili olma odds’u, hiç nodül olmayan hastalarda ilacın etkili olma odds’unun 4.75 katıdır.(Azaltılmış model kullanılmıştır.)
Lojistik regresyonda, 3 veya daha fazla düzeye ait kategorik değişkenleri yorumlarken dikkat edilmesi gereken en önemli nokta “Referans” değerinin doğru bir şekilde tespit edilmesidir. Bizim çalışmamızda bağımsız değişkenimiz 4 düzeyli ve referans düzeyi, hiç nodül olmayan hastalar olarak otomatik belirlenmiştir.
Örnek :
Hastadaki kanser nodülü sağ tarafta(DP2) olan hastalara ait odds oranı için %95’lik aralık kestirimini elde ediniz. Aralık kestirimini kullanarak DP2 değişkenine ait odds oranının anlamlılığını test ediniz.
Sağ tarafta nodülü olan hastalarda ilacın etkili olma odds’u, nodülü olmayan hastalarda ilacın etkili olma oddsunun %95 güvenle en az 1.066 en fazla 4.31 katıdır.
Tahmin edilen OR değerinin anlamlılığını kontrol etmek için 1 değerine eşit olup olmadığına bakılır. Güven aralığı 1 değerini içeriyorsa OR değeri o değişken için anlamsızdır.
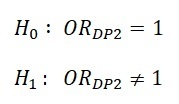
Tahmin ettiğimiz güven aralığı 1 değerini içermiyor, bu sebeple 
hipotezi reddediliyor. Güven aralığı kullanarak test ettiğimiz DP2 değişkenine ait OR değeri, %95 güvenle anlamlıdır.
Not : Uygulamada yazılan tüm fonksiyonlar ve çıktılar görsel olarak verilmiştir. Aşağıda, uygulamada kullanılan fonksiyonlara ulaşabilirsiniz. Ek olarak aynı veri seti üzerinde farklı işlemler yapmak isteyen arkadaşlar bana mail yoluyla ulaşabilirler.
setwd("C:/Users/Asus/Desktop/veribilimiokulu/Fourth Episode/R")
veri <- read.table("veri5_capsule.txt",header = T)
head(veri)
model <- glm(CAPSULE~AGE+RACE+factor(DPROS)+DCAPS+PSA+VOL+GLEASON,
family = binomial,
data = veri)
summary(model)
g <- model$null.deviance-model$deviance
g
df <- model$df.null-model$df.residual
qchisq(p = 0.95,df = df)
ifelse(test = g > df,
yes = "H0 reddedilir, %95 güvenle model anlamlıdır",
no = "H0 reddedilemez, %95 güvenle model anlamlı değildir")
model1 <- glm(CAPSULE~factor(DPROS)+PSA+GLEASON,
family = binomial,
data = veri)
summary(model1)
g <- model1$null.deviance-model1$deviance
g
df <- model1$df.null-model1$df.residual
qchisq(p = 0.95,df = df)
ifelse(test = g>df,
yes = "H0 reddedilir, %95 güvenle model anlamlıdır",
no = "H0 reddedilemez, %95 güvenle model anlamlı değildir")
g_fark <- model1$deviance-model$deviance
tablo <- qchisq(p = 0.95,df = 4)
ifelse(test = g_fark>tablo,
yes = "H0 reddedilir, %95 güvenle model anlamlıdır",
no = "H0 reddedilemez, %95 güvenle model anlamlı değildir")
model$aic
model1$aic
b_PSA <- model1$coefficients["PSA"]
b_PSA
exp(b_PSA)
b_DP3 <- model1$coefficients["factor(DPROS)3"]
b_DP3
exp(b_DP3)
Kır çiçekleri ve manzara seyretmenin önemli bir kusuru var, bedavalar, diye açıkladı. Doğa sevgisiyle fabrikalar çalışmaz. En azından alt sınıflarda doğa sevgisini kaldırmaya karar verildi, ancak ulaşım tüketimi eğilimi kalacaktı. Çünkü elbette nefret etseler de kırlara gitmeye devam etmeleri önemliydi. Sorun, ulaşım tüketimi için kır çiçekleri ve manzara seyretmekten ekonomik olarak daha sağlam bir neden bulmaktı. Gerektiği şekilde bulundu. Müdür, “Kitleleri kırlardan nefret etmeye şartlandırıyoruz,” diye başladı. “Aynı zamanda onları doğa sporlarını sevmeye şartlandırıyoruz. Bunu yaparken de tüm doğa sporlarının gelişmiş aletlerle yapılmasını sağlıyoruz. Böylece hem endüstriyel ürünler, hem de ulaşım tüketiyorlar.”(Huxley, Cesur Yeni Dünya)
Shiny
nyBundan önceki yazılarımda Shiny’de lojistik regresyon uygulamaları yapmıştık. Shiny’nin tam olarak anlaşılabilmesi için bu uygulamaya ara verip, Shiny Eğitim Serisi adı altında bir video serisi çekmeye karar verdim. Bu eğitim serisini hem buradan, hem de Veri Bilimi Okulu Youtube kanalından takip edebilirsiniz.
Giriş
Shiny Nedir? Nasıl Çalışır?
Fonksiyon Yapısı ve “My First Shiny”
Teşekkür
“Yaşları ilerledikçe insanları dine yönelten şeyin ölüm ve ölümden sonraki şeylerin korkusu olduğunu söylerler. Fakat kendi deneyimim beni şu inanca yöneltti: böyle korku ve düşüncelerin apayrı olarak, dini duygular biz yaşlandıkça gelişme eğilimi gösterirler, çünkü ihtiraslarımız ateşini yitirdikçe, hayal güçlerimiz ve duygularımız köreldikçe aklımızı çelen imgeler, arzular ve heveslerden arındıkça Tanrı, gizlendiği bulutların arkasından görünür, ruhumuz bütün aydınlıkların kaynağı olan bu varlığı hisseder, görür ve ona yönelir, bu yöneliş doğal ve kaçınılmazdır; duygular dünyasına canlılığını ve cazibesini veren her şeyi artık yitirmekte olduğumuz için, o muazzam varoluş artık içsel ya da dışsal etkilerle desteklenmediği için, kalıcı bir şeye, bizi aska yanıltmayacak bir şeye tutunma ihtiyacı hissederiz – bir gerçekliğe, mutlak ve ebedi bir gerçeğe tutunmak isteriz. Evet, kaşınılmaz bir biçimde Tanrı’ya yöneliriz; bu dini duygu, doğası gereği öyle saftır ve bunu yaşayan ruha öyle bir mutluluk verir ki, diğer bütün yitirdiklerimizi telafi eder.”(Huxley, Cesur Yeni Dünya)
Değerli zamanınızı ayırdığınız için teşekkürler.
Not: Bundan sonraki yazımda alıntılar yapacağım kitap “Gündüz Vassaf – Cehenneme Övgü” olacaktır. Okumak isteyenlere şiddetle tavsiye ederim 🙂
Lojistik Regresyon için Kaynaklar
https://www.wikiwand.com/en/Least_squares
https://www.wikiwand.com/en/Ordinary_least_squares
https://mysite.science.uottawa.ca/rkulik/mat3378/mat3378-textbook.pdf
http://debis.deu.edu.tr/userweb//kemal.sehirli/dosyalar/regresyon1-2.pdf
https://medium.com/@mehmetberktasmdmsc/odds-oran%C4%B1-odds-ratio-or-bize-ne-anlat%C4%B1yor-f2233963ae9b
Shiny için Kaynaklar
https://shiny.rstudio.com/gallery/widget-gallery.html
https://shiny.rstudio.com/tutorial/written-tutorial/lesson4/
![](https://www.veribilimiokulu.com/wp-content/uploads/2020/05/logo-e1590873495165.png"){kind=logo}